【题目】如图,四边形ABCD,AD∥BC,∠B=90,AD=6,AB=4,BC=9.
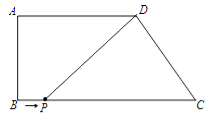
(1)求CD的长为.
(2)点P从点B出发,以每秒1个单位的速度沿着边BC向点C运动,连接DP.设点P运动的时间为t秒,则当t为何值时,△PDC为等腰三角形?
参考答案:
【答案】(1)5(2)①PD=DC, t=3 ②PC=DC, t=5 ③PD=PC, t=65/18
【解析】
试题分析:(1)过点D作![]() ,垂足为
,垂足为![]() ,先判断出四边形
,先判断出四边形![]() 是矩形,在
是矩形,在![]() 中根据勾股定理即可得出
中根据勾股定理即可得出![]() 的长;
的长;
(2) 过点![]() 作
作![]() ,垂足为
,垂足为![]() ,由题意得
,由题意得![]() ,
,![]() .再分
.再分![]() ,
,![]() ,
,![]() 三种情况进行讨论.
三种情况进行讨论.
试题解析:
(1)过点D作![]() ,垂足为E,
,垂足为E,
∵![]() ,
,![]() ,
,
∴四边形ABED是矩形,
∴BE=AD=6,DE=AB=4,
∴CE=BC﹣BE=9﹣6=3,
在Rt△DCE中,![]() .
.
故答案为:5;
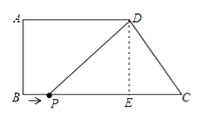
(2)过点D作DE⊥BC,垂足为E,由题意得PC=9﹣t,PE=6﹣t.
当CD=CP时,5=9﹣t,解得t=4;
当CD=PD时,E为PC中点,
∴6﹣t=3,
∴t=3;
当PD=PC时,![]() ,
,
∴![]() ,
,
解得t= ![]() .
.
故t的值为t=3或4或![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一台电视机的原价是2000元,若按原价的八折出售,则购买a台这样的电视机需要元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,抛物线
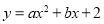 过B(﹣2,6),C(2,2)两点.
过B(﹣2,6),C(2,2)两点.(1)试求抛物线的解析式;
(2)记抛物线顶点为D,求△BCD的面积;
(3)若直线
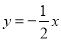 向上平移b个单位所得的直线与抛物线段BDC(包括端点B、C)部分有两个交点,求b的取值范围.
向上平移b个单位所得的直线与抛物线段BDC(包括端点B、C)部分有两个交点,求b的取值范围.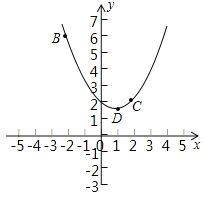
-
科目: 来源: 题型:
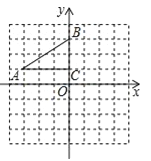
查看答案和解析>>【题目】如图,在平面直角坐标系中,直角△ABC的三个顶点分别是A(﹣3,1),B(0,3),C(0,1)
(1)将△ABC以点C为旋转中心旋转180°,画出旋转后对应的△A1B1C1;
(2)分别连结AB1、BA1后,求四边形AB1A1B的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠C=90°,∠BAC的角平分线AD交BC于点D,若AC=5,BC=12.求点D到AB的距离.

-
科目: 来源: 题型:
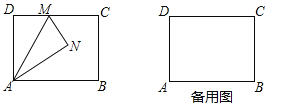
查看答案和解析>>【题目】如图,矩形ABCD中,AB=4,AD=3,M是边CD上一点,将△ADM沿直线AM对折,得到△ANM.
(1)当AN平分∠MAB时,求DM的长;
(2)连接BN,当DM=1时,求△ABN的面积;
(3)当射线BN交线段CD于点F时,求DF的最大值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】八边形的外角和等于 ▲ °.
相关试题

