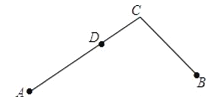
【题目】如果一点在由两条公共端点的线段组成的一条折线上且把这条折线分成长度相等的两部分,这点叫做这条折线的“折中点”.如果点D是折线A﹣C﹣B的“折中点”,请解答以下问题:
(1)已知AC=m,BC=n.
当m>n时,点D在线段 上;
当m=n时,点D与 重合;
当m<n时,点D在线段 上;
(2)若E为线段AC中点,EC=4,CD=3,求CB的长度.
参考答案:
【答案】(1)AC,C,BC;(2)2或14.
【解析】试题分析:(1)根据题意和线段的和差关系即可得到结论;(2)分两种情况求解:①点D在线段AC上,由E为线段AC中点,EC=4,得到AC=2CE=8,于是得到AD=AC-CD=5,根据线段的和差即可得到结论;②点D在线段BC上,由E为线段AC中点,EC=4,得到AC=2CE=8,于是得到AD=AC-CD=5,根据线段的和差即可得到结论.
试题解析:
(1)已知AC=m,BC=n.
当m>n时,点D在线段AC上;
当m=n时,点D与C重合;
当m<n时,点D在线段BC上.
故答案为:AC,C,BC;
(2)点D在线段AC上
∵E为线段AC中点,EC=4,
AC=2CE=8,∵CD=3,
∴AD=AC﹣CD=5,
∵BD=AD=5,
∴BC=5﹣3=2;
点D在线段BC上,
∵E为线段AC中点,EC=4,
∴AC=2CE=8,∵CD=3,
∴AD=AC+CD=11,
∵BD=AD=11,
∴BC=11+3=14.
点睛:本题考查了线段中点的定义及线段的和差倍分的计算,根据图形找出线段之间的关系是解题的关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是一根可伸缩的鱼竿,鱼竿是用10节大小不同的空心套管连接而成.闲置时鱼竿可收缩,完全收缩后,鱼竿长度即为第1节套管的长度(如图1所示):使用时,可将鱼竿的每一节套管都完全拉伸(如图2所示).图3是这跟鱼竿所有套管都处于完全拉伸状态下的平面示意图.已知第1节套管长50cm,第2节套管长46cm,以此类推,每一节套管均比前一节套管少4cm.完全拉伸时,为了使相邻两节套管连接并固定,每相邻两节套管间均有相同长度的重叠,设其长度为xcm.

(1)请直接写出第5节套管的长度;
(2)当这根鱼竿完全拉伸时,其长度为311cm,求x的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列长度的三条线段,不能组成三角形的是( )
A.3,8,4
B.4,9,6
C.15,20,8
D.9,15,8 -
科目: 来源: 题型:
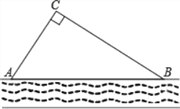
查看答案和解析>>【题目】某校生物兴趣小组把一块沿河的三角形废地(如图)开辟为生物园(设AB段河岸为直线),已知∠ACB=90°,∠CAB=55°,BC=80米,学校决定在点C处建一个蓄水池,利用管道从河中取水,已知每铺设1米管道费用为50元,求铺设管道的最低费用(精确到1元).(参考数据:sin55°≈0.82,cos55°≈0.57,tan55°≈1.43)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,直线AB:y=kx﹣2与y轴相交于点A,与反比例函数y=
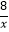 在第一象限内的图象相交于点B(m,2).
在第一象限内的图象相交于点B(m,2). 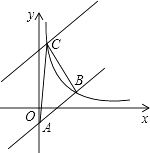
(1)求直线AB的表达式;
(2)将直线AB向上平移后与反比例函数图象在第一象限内交于点C,且△ABC的面积为18,求平移后的直线的表达式. -
科目: 来源: 题型:
查看答案和解析>>【题目】母亲节前夕,某淘宝店主从厂家购进A、B两种礼盒,已知A、B两种礼盒的单价比为2:3,单价和为200元.
(1)求A、B两种礼盒的单价分别是多少元?
(2)该店主购进这两种礼盒恰好用去9600元,且购进A种礼盒最多36个,B种礼盒的数量不超过A种礼盒数量的2倍,共有几种进货方案?
(3)根据市场行情,销售一个A种礼盒可获利10元,销售一个B种礼盒可获利18元.为奉献爱心,该店主决定每售出一个B种礼盒,为爱心公益基金捐款m元,每个A种礼盒的利润不变,在(2)的条件下,要使礼盒全部售出后所有方案获利相同,m值是多少?此时店主获利多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:在矩形ABCD中,AB=8,BC=12,四边形EFGH的三个顶点E、F、H分别在矩形ABCD边AB、BC、DA上,AE=2.
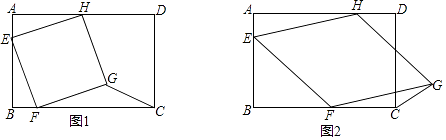
(1)如图1,当四边形EFGH为正方形时,求△GFC的面积;
(2)如图2,当四边形EFGH为菱形时,设BF=x,△GFC的面积为S,求S关于x的函数关系式,并写出函数的定义域.
相关试题

