【题目】某商场准备进一批两种不同型号的衣服,已知购进A种型号衣服9件,B种型号衣服10件,则共需1810元;若购进A种型号衣服12件,B种型号衣服8件,共需1880元;已知销售一件A型号衣服可获利18元,销售一件B型号衣服可获利30元,要使在这次销售中获利不少于699元,且A型号衣服不多于28件.
(1)求A、B型号衣服进价各是多少元?
(2)若已知购进A型号衣服是B型号衣服的2倍还多4件,则商店在这次进货中可有几种方案并简述购货方案.
【答案】(1)A种型号的衣服每件90元,B种型号的衣服100元;(2)有三种进货方案,具体见解析.
【解析】试题分析:(1)等量关系为:A种型号衣服9件×进价+B种型号衣服10件×进价=1810,A种型号衣服12件×进价+B种型号衣服8件×进价=1880;
(2)关键描述语是:获利不少于699元,且A型号衣服不多于28件.关系式为:18×A型件数+30×B型件数≥699,A型号衣服件数≤28.
试题解析:(1)设A种型号的衣服每件x元,B种型号的衣服y元,
则:![]() ,
,
解之得![]() .
.
答:A种型号的衣服每件90元,B种型号的衣服100元;
(2)设B型号衣服购进m件,则A型号衣服购进(2m+4)件,
可得:![]() ,
,
解之得192m12,
∵m为正整数,
∴m=10、11、12,2m+4=24、26、28.
答:有三种进货方案:
(1)B型号衣服购买10件,A型号衣服购进24件;
(2)B型号衣服购买11件,A型号衣服购进26件;
(3)B型号衣服购买12件,A型号衣服购进28件。
点睛:点睛:本题主要考查二元一次方程组和一元一次不等式组的实际问题的应用,解题的关键是读懂题目的意思,根据题目给出的条件,设出未知数,分别找出甲组和乙组对应的工作时间,找出合适的等量关系,列出方程组,再求解.
【题型】解答题
【结束】
21
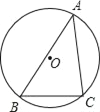
【题目】如图,锐角△ABC内接于⊙O,若⊙O的半径为6,sinA=![]() ,求BC的长.
,求BC的长.
参考答案:
【答案】BC=8.
【解析】试题分析:通过作辅助线构成直角三角形,再利用三角函数知识进行求解.
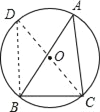
试题解析:作⊙O的直径CD,连接BD,则CD=2×6=12.
∵![]()
∴![]()
∴![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,是两种长方形铝合金窗框,已知窗框的长都是y米,窗框的宽都是x米,若一用户需(1)型的窗框2个,(2)型的窗框2个.
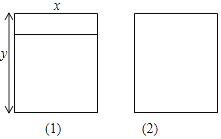
(1)用含x、y的式子表示共需铝合金的长度;
(2)若1m铝合金的平均费用为100元,求当x=1.2,y=1.5时,铝合金的总费用为多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】将一些长30厘米,宽10厘米的长方形纸,按图所示方法粘合起来,粘合部分的宽为2厘米.

(1)求5张白纸粘合后的总长度为多少厘米?
(2)设x张白纸粘合后的总长度为y厘米,请写出y与x之间的关系式?
(3)求当x=20时,试求y的值为多少.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点P(x0,y0)和直线y=kx+b,则点P到直线y=kx+b的距离证明可用公式d=
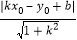 计算.
计算.例如:求点P(﹣1,2)到直线y=3x+7的距离.
解:∵直线y=3x+7,其中k=3,b=7.
∴点P(﹣1,2)到直线y=3x+7的距离为:
d=
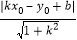 =
=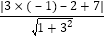 =
= =
=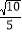 .
.根据以上材料,解答下列问题:
(1)求点P(﹣1,3)到直线y=x﹣3的距离;
(2)已知⊙Q的圆心Q坐标为(0,3),半径r为3,判断⊙Q与直线y=
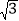 x+9的位置关系并说明理由;
x+9的位置关系并说明理由;(3)已知直线y=3x+3与y=3x﹣6平行,求这两条直线之间的距离.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,C是AB上一点,点D,E分别在AB两侧,AD∥BE,且AD=BC,BE=AC.

(1)求证:CD=CE;
(2)连接DE,交AB于点F,猜想△BEF的形状,并给予证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】目前“微信”、“支付宝”、“共享单车”和“网购”给我们带来了很多便利,初二数学小组在校内对“你最认可的四大新生事物”进行了调查,随机调查了
 人(每名学生必选一种且只能从这四种中选择一种)并将调查结果绘制成如下不完整的统计图.
人(每名学生必选一种且只能从这四种中选择一种)并将调查结果绘制成如下不完整的统计图.
(1)根据图中信息求出
 =___________,
=___________, =_____________;
=_____________;(2)请你帮助他们将这两个统计图补全;
(3)根据抽样调查的结果,请估算全校2000名学生种,大约有多少人最认可“微信”这一新生事物?
-
科目: 来源: 题型:
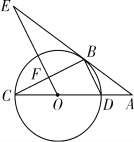
查看答案和解析>>【题目】如图所示,CD为⊙O的直径,点B在⊙O上,连接BC、BD,过点B的切线AE与CD的延长线交于点A,OE∥BD,交BC于点F,交AB于点E.
(1)求证:∠E=∠C;
(2)若⊙O的半径为3,AD=2,试求AE的长;
(3)求△ABC的面积.
相关试题

