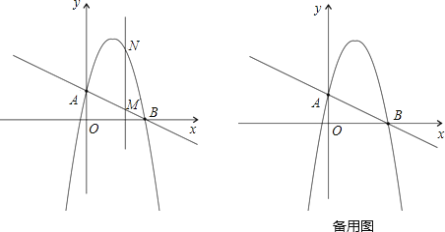
【题目】如图,一次函数y=-![]() x+2分别交y轴、x轴于A、B两点,抛物线y=-
x+2分别交y轴、x轴于A、B两点,抛物线y=-![]() +bx+c过A、B两点.
+bx+c过A、B两点.
(1)求这个抛物线的解析式;
(2)作垂直x轴的直线x=t,在第一象限交直线AB于M,交这个抛物线于N.求当t取何值时,MN有最大值?最大值是多少?
(3)在(2)的情况下,以A、M、N、D为顶点作平行四边形,求第四个顶点D的坐标.
参考答案:
【答案】(1)、y=-![]() +3.5x+2;(2)、t=2时,最大值为4;(3)、(0,6),(0,-2)或(4,4)
+3.5x+2;(2)、t=2时,最大值为4;(3)、(0,6),(0,-2)或(4,4)
【解析】
试题分析:(1)、根据题意得出点A和点B的坐标,然后将两点代入函数解析式得出b和c的值,得出函数解析式;(2)、设出点M和点N的坐标,从而得出MN的长度,根据二次函数的性质得出最大值;(3)、根据题意得出点A、点M和点N的坐标,然后根据平行四边形的性质得出三种情况,从而求出点D的坐标.
试题解析:(1)、求A、B点的坐标为:A(0,2),B(4,0) 将x=0,y=2代入y=-![]() +bx+c得c=2
+bx+c得c=2
将x=4,y=0代入y=-![]() +bx+c得0=-16+4b+2,解得b=3.5
+bx+c得0=-16+4b+2,解得b=3.5
∴抛物线解析式为:y=-![]() +3.5x+2
+3.5x+2
(2)、由题意,易得M(t,-![]() t+2), N(t, -
t+2), N(t, -![]() +3.5t+2),从而MN=-
+3.5t+2),从而MN=-![]() +3.5t+2-(-
+3.5t+2-(-![]() t+2)=-
t+2)=-![]() +4t=-
+4t=-![]()
∴当t=2时,MN有最大值4
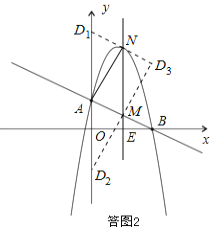
(3) 、由(2)可知,A(0,2),M(2,1),N(2,5).
以A、M、N、D为顶点作平行四边形,D点的可能位置有三种情形,如答图2所示.
当D在y轴上时,设D的坐标为(0,a) 由AD=MN,得|a-2|=4,解得![]() =6,
=6,![]() =-2,
=-2,
从而D为(0,6)或D(0,-2)
当D不在y轴上时,由图可知D3为D1N与D2M的交点,求出直线D1N与D2M的解析式
由两解析式联立解得D为(4,4) 故所求的D点坐标为(0,6),(0,-2)或(4,4)
-
科目: 来源: 题型:
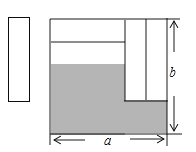
查看答案和解析>>【题目】如图,把四张形状大小完全相同的小长方形卡片不重叠地放在一个底面为长方形(长为a , 宽为b)的盒子底部,盒子底面未被卡片覆盖的部分用阴影表示,则这两块阴影部分小长方形周长的和为( )
A.a+2b
B.4a
C.4b
D.2a+b -
科目: 来源: 题型:
查看答案和解析>>【题目】某快递员准备送出一批美术用纸共25500包,其中包括素描纸、手工彩色卡纸和水粉纸三种美术用纸,它们的数量比为1:2:14.该快递员准备送出的这三种美术用纸各多少包?
-
科目: 来源: 题型:
查看答案和解析>>【题目】把命题“等角的补角相等”改写成“如果…那么…”的形式是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】到三角形三个顶点的距离都相等的点是这个三角形的( )
A.三条高的交点
B.三条角平分线的交点
C.三条中线的交点
D.三条边的垂直平分线的交点 -
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式3m4﹣48= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个正数x的两个不同的平方根是3a﹣4和1﹣6a,求a及x的值.
相关试题

