Question

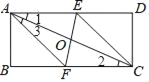
【题目】已知如图所示的一张平行四边形纸片ABCD（AD＞AB），将纸片折叠一次，使点A与点C重合，再展开，折痕EF交AD边于点E，交BC边于点F，分别连结AF和CE．

（1）求证：四边形AFCE是菱形．

（2）若AB=8cm，∠B=90°，△ABF的面积为24cm2，求菱形AFCE的周长．

Answer 1

【答案】（1）见解析；（2）菱形AFCE的周长为40cm．

【解析】试题分析： （1）由折叠可得EA=EC，FA=FC，∠2=∠3；由四边形ABCD为平行四边形可得∠1=∠2，根据等量代换可得∠1=∠3，由三线合一知△AEF为等腰三角形，所以AE=AF，从而可证四边形AFCE是菱形；

（2）由△ABF的面积为24cm2和AB=8cm，根据三角形面积公式可求出BF=6cm，利用勾股定理求出AF=10cm，从而可求出菱形的周长.

（1）证明：∵将平行四边形ABCD（AD＞AB）折叠，使点A与点C重合，

∴EF垂直平分AC，

∴EA=EC，FA=FC，

∴∠2=∠3，

∵四边形ABCD为平行四边形，

∴AD∥BC，

∴∠1=∠2，

∴∠1=∠3，

∵AO⊥EF，

∴△AEF为等腰三角形，

∴AE=AF，

∴AE=EC=AF=CF，

∴四边形AFCE是菱形；

（2）解：在Rt△ABF中，∵ABBF=24，AB=8cm，

∴BF=6cm，

∴AB2+BF2=AF2=100，

∴AF=10cm，

∴菱形AFCE的周长为10×4=40（cm）．

故菱形AFCE的周长为40cm．