【题目】问题探究:
(1)如图①,边长为4的等边△OAB位于平面直角坐标系中,将△OAB折叠,使点B落在OA的中点处,则折痕长为;
(2)如图②,矩形OABC位于平面直角坐标系中,其中OA=8,AB=6,将矩形沿线段MN折叠,点B落在x轴上,其中AN= ![]() AB,求折痕MN的长;
AB,求折痕MN的长;
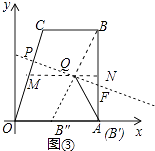
(3)如图③,四边形OABC位于平面直角坐标系中,其中OA=AB=6,CB=4,BC∥OA,AB⊥OA于点A,点Q(4,3)为四边形内部一点,将四边形折叠,使点B落在x轴上,问是否存在过点Q的折痕,若存在,求出折痕长,若不存在,请说明理由.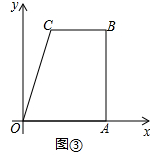
参考答案:
【答案】
(1)2
(2)
解:如图2中,B的对称点B′,折痕为MN,MN交BB′于H
∵AN= ![]() AB=2,
AB=2,
∴NB=NB′=4,
在Rt△ANB′中,AB′= ![]() =2
=2 ![]() ,
,
∴OB′=8﹣2 ![]() ,
,
∴点B′(8﹣2 ![]() ,0),
,0),
∵B(8,6),
∴BB′中点H(8﹣ ![]() ,3),∵点N坐标(8,2),
,3),∵点N坐标(8,2),
设直线NH解析式为y=kx+b,则有 ![]() 解得
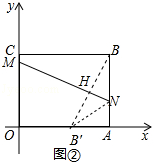
解得 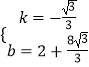 ,
,
∴直线NH解析式为y=﹣ ![]() x+2+
x+2+ ![]() ,
,
∴点M坐标(0,2+ ![]() ),
),
∴MN= ![]() =
= ![]()
(3)
解:存在.
理由:如图3中,延长BQ交OA于B″,连接AQ,过点Q作MN∥OA,交OC于M,交AB于N.
∵Q(4,3),
∴N(6,3),
∴BN=AN.QB=QB″,
作BB″的垂直平分线PF,交OC于P,交AB于F,此时B、B″关于直线PF对称,满足条件,
在Rt△ABB″中,∵∠BAB″=90°,BQ=QB″,
∴AQ=QB,
∴此时B、A(B′)关于直线MN对称,满足条件.
∵C(2,6),
∴直线OC解析式为y=3x,
∵NM∥OA,BN=NA,
∴CM=OM,
∴点M(1,3),
∴MN=5(过M做MM'⊥BA于M',利用△BB'A中AB'=2√3,AB=6,所以∠B'BA=30°,进而推导∠M'MN=30°,求得MN结果更快!)
∵B(6,6),B″(2,0),
∴可得直线BB″的解析式为y= ![]() x﹣3,
x﹣3,
∴过点Q垂直BB″的直线PF的解析式为y=﹣ ![]() x+
x+ ![]() ,
,
由 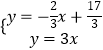 解得
解得 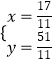 ,
,
∴点P( ![]() ,
, ![]() ),F(6,
),F(6, ![]() ),
),
∴PF= ![]() =
= ![]() ,
,
综上所述,折痕的长为5或 ![]()
【解析】解:(1)如图1中,B的对称点B′,折痕为MN,MN交BB′于H.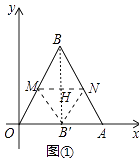
∵△ABC是等边三角形,OB′=B′A,
∴BB′⊥OA,又∵BB′⊥MN,
∴MN∥OA,∵BH=HB′,
∴BM=OM,BN=NA,
∴MN是△ABC的中位线,
∴MN= ![]() OA=2.
OA=2.
故答案为2.
(1)如图1中,B的对称点B′,折痕为MN,MN交BB′于H.只要证明折痕是△ABC的中位线即可.(2)如图2中,B的对称点B′,折痕为MN,MN交BB′于H,求出直线MN的解析式即可解决问题.(3)存在.如图3中,延长BQ交OA于B″,连接AQ,过点Q作MN∥OA,交OC于M,交AB于N.可以证明线段MN计算折痕;作BB″的垂直平分线PF,交OC于P,交AB于F,此时B、B″关于直线PF对称,线段PF也是折痕.分别求出MN、PF即可解决问题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC,以AB为直径的⊙O分别交AC于D,BC于E,连接ED,若ED=EC.
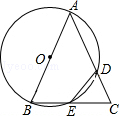
(1)求证:AB=AC;
(2)若AB=4,BC=2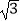 ,求CD的长.
,求CD的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,抛物线y=x2+bx+c经过A、B两点,A、B两点的坐标分别为(﹣1,0)、(0,﹣3).
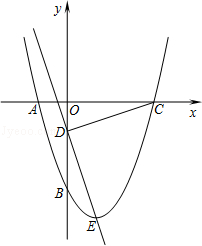
(1)求抛物线的函数解析式;
(2)点E为抛物线的顶点,点C为抛物线与x轴的另一交点,点D为y轴上一点,且DC=DE,求出点D的坐标;
(3)在第二问的条件下,在直线DE上存在点P,使得以C、D、P为顶点的三角形与△DOC相似,请你直接写出所有满足条件的点P的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:关于x的一元二次方程kx2﹣(4k+1)x+3k+3=0(k是整数).
(1)求证:方程有两个不相等的实数根;
(2)若方程的两个实数根都是整数,求k的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中(如图每格一个单位),描出下列各点A(﹣2,﹣1),B(2,﹣1),C(2,2),D(3,2),E(0,3),F(﹣3,2),G(﹣2,2),A(﹣2,﹣1)并依次将各点连接起来,观察所描出的图形,它像什么?根据图形回答下列问题:
(1)图形中哪些点在坐标轴上,它们的坐标有什么特点?
(2)线段FD和x轴有什么位置关系?点F和点D的坐标有什么特点?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,方格纸中每个小方格都是长为1个单位的正方形,若学校位置坐标为A(1,2),解答以下问题:
(1)请在图中建立适当的直角坐标系,并写出图书馆B位置的坐标;

(2)若体育馆位置坐标为C(-3,3),请在坐标系中标出体育馆的位置,并顺次连接学校、图书馆、体育馆,得到△ABC,求△ABC的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,AC=BC=4,CD⊥AB于D,P是线段CD上一个动点,以P为直角顶点向下作等腰Rt△BPE,连结AE,DE.
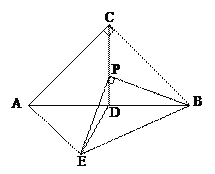
(1)∠BAE的度数是否为定值?若是,求出∠BAE的度数;
(2)直接写出DE的最小值。
相关试题

