Question

【题目】如图，AB交CD于O，OE⊥AB．

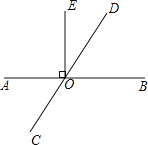
（1）若∠EOD=30°，求∠AOC的度数；

（2）若∠AOC：∠BOC=2：3，求∠EOD的度数．

Answer 1

【答案】（1）60°（2）18°

【解析】

试题分析：（1）利用垂直可先求得∠BOD，再根据对顶角相等可求得∠AOC；

（2）由条件可先求得∠AOC，再利用对顶角相等可求得∠BOD，再由垂直的定义可求得∠EOD．

解：

（1）∵OE⊥AB，

∴∠EOB=90°，

又∵∠EOD=30°，

∴∠BOD=60°，

又∵∠BOD=∠AOC （对顶角相等），

∴∠AOC=60°；

（2）∵∠AOC+∠BOC=180°，

若∠AOC：∠BOC=2：3，

∴∠AOC=×180°=72°，

又∵∠BOD=∠AOC （对顶角相等），

∴∠BOD=72°，

∴∠EOD=90°﹣72°=18°．