搜索
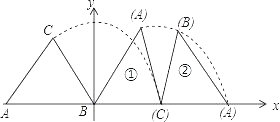
【题目】等腰三角形ABC在平面直角坐标系中的位置如图所示，已知点A（﹣6，0），点B在原点，CA=CB=5，把等腰三角形ABC沿x轴正半轴作无滑动顺时针翻转，第一次翻转到位置①，第二次翻转到位置②…依此规律，第18次翻转后点C的纵坐标是_____．
参考答案：
【答案】4
【解析】
根据题意可知每翻折三次与初始位置的形状相同，第15次与开始时形状相同，故以点B为参照点，第15次的坐标减去3即可得此时点C的横坐标．
解：过C作CD⊥AB于D，
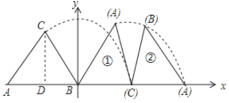
∵A（-6，0），点B在原点，CA=CB=5，
∴AB=6，
∴BD=3，
∴CD=4，
∴C（-3，4），
由题意可得，每翻转三次与初始位置的形状相同，
18÷3=6，
故第18次翻转后点C的纵坐标是：4，
故答案为：4．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如果一个正整数能表示成两个连续偶数的平方差，那么这个正整数为“神秘数”.
如：
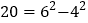
因此，4，12，20这三个数都是神秘数.
（1）28和2012这两个数是不是神秘数？为什么？
（2）设两个连续偶数为
和
(其中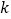
为非负整数)，由这两个连续偶数构造的神秘数是4的倍数，请说明理由. （3）两个连续奇数的平方差（取正数）是不是神秘数？请说明理由.
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知△ABC，点D、F分别为线段AC、AB上两点，连接BD、CF交于点E．
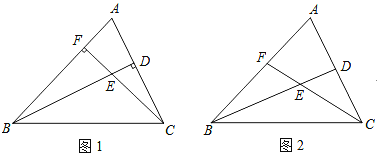
（1）若BD⊥AC，CF⊥AB，若BE=4，CE=2，求CD：BF；
（2）若BD平分∠ABC，CF平分∠ACB，如图2所示，猜想∠BEC与∠A的数量关系；并说明理由．
（3）在（2）的条件下，若∠A=60°，试说明：BC=BF+CD．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，E，F分别是ABCD的边AD，BC上的点，EF=6，∠DEF=60°，将四边形EFCD沿EF翻折得到EFC′D′，ED′交BC于点C，则△GEF的周长为_____．
-
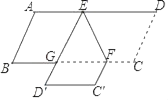
科目： 来源： 题型：
查看答案和解析>>【题目】（8分）如图，在ABCD中，∠BCD=120°，分别延长DC、BC到点E，F，使得△BCE和△CDF都是正三角形．
（1）求证：AE=AF；
（2）求∠EAF的度数．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在菱形ABCD中，AB=4cm，∠ADC=120°，点E、F同时由A、C两点出发，分别沿AB、CB方向向点B匀速移动（到点B为止），点E的速度为1cm/s，点F的速度为2cm/s，经过t秒△DEF为等边三角形，则t的值为 ．
-
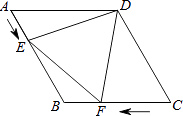
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系中，A、B两点分别在x轴和y轴上，OA=1，OB=
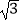，连接AB，过AB中点C1分别作x轴和y轴的垂线，垂足分别是点A1、B1 ， 连接A1B1 ， 再过A1B1中点C2作x轴和y轴的垂线，照此规律依次作下去，则点Cn的坐标为 ．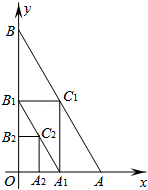 
相关试题
