【题目】已知△ABC,点D、F分别为线段AC、AB上两点,连接BD、CF交于点E.
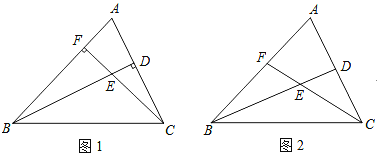
(1)若BD⊥AC,CF⊥AB,若BE=4,CE=2,求CD:BF;
(2)若BD平分∠ABC,CF平分∠ACB,如图2所示,猜想∠BEC与∠A的数量关系;并说明理由.
(3)在(2)的条件下,若∠A=60°,试说明:BC=BF+CD.
参考答案:
【答案】(1)1:2(2)∠BEC=90°+![]() ∠A(3)证明见解析
∠A(3)证明见解析
【解析】
(1)根据∠BEF=∠CED,∠BFE=∠CDE=90°可证明△BEF∽△CED,根据相似三角形的性质即可得答案;(2)根据角平分线的性质得到∠EBC=![]() ∠ABC,∠ECB=
∠ABC,∠ECB=![]() ∠ACB,根据三角形内角和定理即可得到结论;(3)在BC上截取BM=BF,连接EM,根据SAS可证明△BEF≌△BEM,可得∠BEF=∠BEM,由(2)可得∠BEC=120°,即可证∠∠BEF=∠BEM=∠CEM=∠CED=60°,即可证明△CEM≌△CED,进而可得CD=CM,即可证明BC=BF+CD.
∠ACB,根据三角形内角和定理即可得到结论;(3)在BC上截取BM=BF,连接EM,根据SAS可证明△BEF≌△BEM,可得∠BEF=∠BEM,由(2)可得∠BEC=120°,即可证∠∠BEF=∠BEM=∠CEM=∠CED=60°,即可证明△CEM≌△CED,进而可得CD=CM,即可证明BC=BF+CD.
(1)∵∠BEF=∠CED,∠BFE=∠CDE=90°,
∴△BEF∽△CED,
∴![]()
∵BE=4,CE=2,
∴CD:BF=1:2.
(2)∠BEC =90°+![]() ∠A;理由如下:
∠A;理由如下:
∵BD平分∠ABC,CF平分∠ACB,
∴∠EBC=![]() ∠ABC,∠ECB=
∠ABC,∠ECB=![]() ∠ACB,
∠ACB,
∴∠BEC=180°-![]() (∠ABC+∠ACB),
(∠ABC+∠ACB),
∵∠ABC+∠ACB=180°-∠A,
∴∠BEC=180°-![]() (180°-∠A)=90°+∠A.
(180°-∠A)=90°+∠A.
(3)如图:在BC上截取BM=BF,连接EM,
∵∠A=60°,
∴由(2)可知∠BEC=90°+![]() ∠A=120°,
∠A=120°,
∴∠BEF=60°,
∵BE平分∠ABC,
∴∠FBE=∠EBM,
∵BF=BM,∠FBE=∠EBM,BE=BE,
∴△BEF≌△BEM(SAS),
∴∠BEM=∠BEF=60°,
∴∠CEM=60°,
∴∠CED=∠CEN=60°,
∵CE平分∠ACB,
∴∠DCE=∠MCE,
∵∠CED=∠CEN=60°,CE=CE,∠DCE=∠MCE,
∴△CEM≌△CED(ASA),
∴CD=CM,
∴BC=BM+CM=BF+CD.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)已知2x﹣y=8,求代数式[x2+y2﹣(x﹣y)2+2y(x﹣y)]÷4y的值.
(2)阅读下列材料:常用分解因式的方法有提取公因式法、公式法,但有部分多项式只单纯用上述方法就无法分解,如x2﹣2xy+y2﹣16,我们细心观察这个式子就会发现,前三项符合完全平方公式,进行变形后可以与第四项结合再运用平方差公式进行分解.过程如下:x2﹣2xy+y2﹣16=(x﹣y)2﹣16=(x﹣y+4)(x﹣y﹣4)这种分解因式的方法叫分组分解法.利用这种分组的思想方法解决下列问题:
已知a,b,c分别是△ABC三边的长,且2a2+b2+c2﹣2a(b+c)=0请判断△ABC的形状,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图①,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,求证:∠ACD=∠B;
(2)如图②,在Rt△ABC中,∠C=90°,D、E分别在AC,AB上,且∠ADE=∠B,判断△ADE的形状?并说明理由?
(3)如图③,在Rt△ABC和Rt△DBE中,∠C=90°,∠E=90°,点C,B,E在同一直线上,若AB⊥BD,AB=BD,则CE与AC,DE有什么等量关系,并证明.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如果一个正整数能表示成两个连续偶数的平方差,那么这个正整数为“神秘数”.
如:


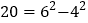
因此,4,12,20这三个数都是神秘数.
(1)28和2012这两个数是不是神秘数?为什么?
(2)设两个连续偶数为
 和
和 (其中
(其中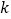 为非负整数),由这两个连续偶数构造的神秘数是4的倍数,请说明理由.
为非负整数),由这两个连续偶数构造的神秘数是4的倍数,请说明理由. (3)两个连续奇数的平方差(取正数)是不是神秘数?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,E,F分别是ABCD的边AD,BC上的点,EF=6,∠DEF=60°,将四边形EFCD沿EF翻折得到EFC′D′,ED′交BC于点C,则△GEF的周长为_____.
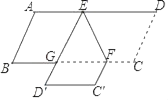
-
科目: 来源: 题型:
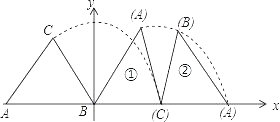
查看答案和解析>>【题目】等腰三角形ABC在平面直角坐标系中的位置如图所示,已知点A(﹣6,0),点B在原点,CA=CB=5,把等腰三角形ABC沿x轴正半轴作无滑动顺时针翻转,第一次翻转到位置①,第二次翻转到位置②…依此规律,第18次翻转后点C的纵坐标是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(8分)如图,在ABCD中,∠BCD=120°,分别延长DC、BC到点E,F,使得△BCE和△CDF都是正三角形.

(1)求证:AE=AF;
(2)求∠EAF的度数.
相关试题

