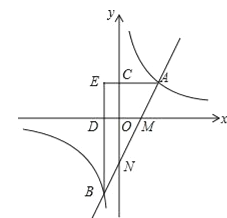
【题目】如图,直线y=2x﹣2分别与x轴、y轴相交于M,N两点,并且与双曲线y=![]() (k>0)相交于A,B两点,过点A作AC⊥y轴于点C,过点B作BD⊥x轴于点D,AC与BD的延长线交于点E(m,n).
(k>0)相交于A,B两点,过点A作AC⊥y轴于点C,过点B作BD⊥x轴于点D,AC与BD的延长线交于点E(m,n).
(1)求证:![]() ;
;
(2)若![]() ,求
,求![]() >2x﹣2的x的取值范围;
>2x﹣2的x的取值范围;
(3)在(2)的条件下,P为双曲线上一点,以OB,OP为邻边作平行四边形,且平行四边形的周长最小,求第四个顶点Q的坐标.
参考答案:
【答案】(1)、证明过程见解析;(2)、x<﹣1或0<x<2;(3)、P(2,2)或(﹣2,﹣2),Q(1,﹣2)或(﹣3,﹣6).
【解析】
试题分析:(1)、设A(x1,![]() ),B(x2,
),B(x2,![]() ),则有AE=x1﹣x2,BE=
),则有AE=x1﹣x2,BE=![]() ﹣
﹣![]() ,EC=﹣x2,ED=
,EC=﹣x2,ED=![]() ,首先证明
,首先证明![]() =
=![]() ,由此即可解决问题.(2)、由DM∥AE,得
,由此即可解决问题.(2)、由DM∥AE,得![]() =
=![]() =
=![]() ,设A(m,n)则B(﹣
,设A(m,n)则B(﹣![]() ,﹣2n),把A、B代入y=2x﹣2得到:
,﹣2n),把A、B代入y=2x﹣2得到:![]() ,解得:
,解得:![]() ,求出A、B两点坐标即可解决问题.(3)、因为点B是定点,OB是定长,所以要求平行四边形OBPQ的周长的最小值只需要求出OP的最小值即可,由P在y=
,求出A、B两点坐标即可解决问题.(3)、因为点B是定点,OB是定长,所以要求平行四边形OBPQ的周长的最小值只需要求出OP的最小值即可,由P在y=![]() 上,设P(a,
上,设P(a,![]() ),因为OP2=n2+
),因为OP2=n2+![]() =(n﹣
=(n﹣![]() )2+8,所以当n﹣
)2+8,所以当n﹣![]() =0时,OP2的值最小,由此即可解决问题.
=0时,OP2的值最小,由此即可解决问题.
试题解析:(1)、设A(x1,![]() ),B(x2,
),B(x2,![]() ),则有AE=x1﹣x2,BE=
),则有AE=x1﹣x2,BE=![]() ﹣
﹣![]() ,EC=﹣x2,ED=
,EC=﹣x2,ED=![]() ,
,
∴![]() =
=![]() , ∴
, ∴![]() =
=![]() .
.
(2)、∵DM∥AE, ∴![]() , ∴A(m,n)则B(﹣
, ∴A(m,n)则B(﹣![]() ,﹣2n),
,﹣2n),
把A、B代入y=2x﹣2得到![]() , 解得
, 解得![]() , ∴A(2,2),B(﹣1,﹣4),
, ∴A(2,2),B(﹣1,﹣4),
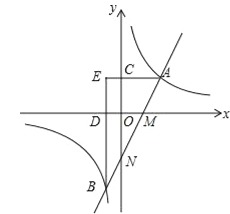
由图象可知,![]() >2x﹣2时,x<﹣1或0<x<2.
>2x﹣2时,x<﹣1或0<x<2.
(3)、由(2)可知反比例函数解析式为y=![]() ,A(2,2),B(1,﹣4), ∵四边形OBPQ是平行四边形,
,A(2,2),B(1,﹣4), ∵四边形OBPQ是平行四边形,
∴OB=PQ,PO=BQ, ∵点B是定点,∴OB是定长, ∴要求平行四边形OBPQ的周长的最小值只需要求出OP的最小值即可, ∵P在y=![]() 上,设P(a,
上,设P(a,![]() ), ∴OP2=n2+
), ∴OP2=n2+![]() =(n﹣
=(n﹣![]() )2+8,
)2+8,
∴当n﹣![]() =0时,OP2的值最小, ∴n=±2时,OP有最小值, ∴P(2,2)或(﹣2,﹣2),Q(1,﹣2)或(﹣3,﹣6).
=0时,OP2的值最小, ∴n=±2时,OP有最小值, ∴P(2,2)或(﹣2,﹣2),Q(1,﹣2)或(﹣3,﹣6).
-
科目: 来源: 题型:
查看答案和解析>>【题目】若x=﹣1是关于x的方程ax+1=2的解,则a的值为_____.
-
科目: 来源: 题型:
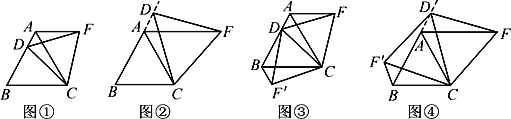
查看答案和解析>>【题目】(1)操作发现:如图①,D是等边△ABC的边BA上一动点(点D与点B不重合),连接DC,以DC为边在BC上方作等边△DCF,连接AF,你能发现AF与BD之间的数量关系吗?并证明你发现的结论;
(2)类比猜想:如图②,当动点D运动至等边△ABC边BA的延长线时,其他作法与(1)相同,猜想AF与BD在(1)中的结论是否仍然成立?
(3)深入探究:Ⅰ.如图③,当动点D在等边△ABC边BA上运动时(点D与B不重合),连接DC,以DC为边在BC上方和下方分别作等边△DCF和等边△DCF′,连接AF,BF′,探究AF,BF′与AB有何数量关系?并证明你的探究的结论;Ⅱ.如图④,当动点D在等边△ABC的边BA的延长线上运动时,其他作法与图③相同,Ⅰ中的结论是否成立?若不成立,是否有新的结论?并证明你得出的结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列单项式:﹣a,2a2 , ﹣3a3 , 4a4 , ﹣5a5 , …可以得到第2016个单项式是;第n个单项式是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB,CD相交于点O,射线OM平分∠AOC,ON⊥OM,若∠AOM=35°,则∠CON的度数为( )

A.35°
B.45°
C.55°
D.65° -
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆锥的底面半径长为8,侧面展开后得到一个半圆,则该圆锥的母线长为_________.
-
科目: 来源: 题型:
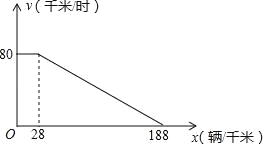
查看答案和解析>>【题目】“城市发展 交通先行”,成都市今年在中心城区启动了缓堵保畅的二环路高架桥快速通道建设工程,建成后将大大提升二环路的通行能力.研究表明,某种情况下,高架桥上的车流速度V(单位:千米/时)是车流密度x(单位:辆/千米)的函数,且当0<x≤28时,V=80;当28<x≤188时,V是x的一次函数.函数关系如图所示.
(1)求当28<x≤188时,V关于x的函数表达式;
(2)若车流速度V不低于50千米/时,求当车流密度x为多少时,车流量P(单位:辆/时)达到最大,并求出这一最大值.
(注:车流量是单位时间内通过观测点的车辆数,计算公式为:车流量=车流速度×车流密度)
相关试题

