Question

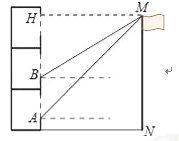
【题目】如图，小明所在教学楼的每层高度为3.5米，为了测量旗杆MN的高度，他在教学楼一楼的窗台A处测得旗杆顶部M的仰角为45°，他在二楼窗台B处测得M的仰角为31°，已知每层楼的窗台离该层的地面高度均为1米，求旗杆MN的高度；（结果保留两位小数）

（参考数据：sin31°≈0.52，cos31°≈0.86，tan31°≈0.60）

Answer 1

【答案】旗杆MN的高度度约为9.75米．

【解析】

试题分析：过点M的水平线交直线AB于点H，设MH=x，则AH=x，结合等腰直角三角形的性质和解直角三角形ABH得到AB=AH﹣BH=x﹣0.60x=0.4x=3.5，由此求得MH的长度，则MN=AB+BH．

试题解析：过点M的水平线交直线AB于点H，

由题意，得∠AMH=∠MAH=45°，∠BMH=31°，AB=3.5，

设MH=x，则AH=x，BH=xtan31°=0.60x，

∴AB=AH﹣BH=x﹣0.60x=0.4x=3.5，

解得x=8.75，

则旗杆高度MN=x+1=9.75（米）

答：旗杆MN的高度度约为9.75米．