搜索
【题目】课本例题
已知：如图，AD是
的角平分线，
，
，垂足分别为E、F．求证：AD垂直平分EF．
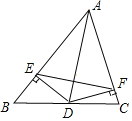
小明做法
证明：因为AD是的角平分线，，，所以
理由是：“角平分线上的点到这个角的两边的距离相等”．
因为，
所以AD垂直平分EF．
理由是：“到线段两个端点距离相等的点在这条线段的垂直平分线上”．
老师观点
老师说：小明的做法是错误的
请你解决
指出小明做法的错误；
正确、完整的解决这道题．
参考答案：
【答案】
见解析；
见解析.
【解析】
小明证明
不能说明AD垂直平分EF，只有再证明
时，A也在EF的垂直平分线上，两点确定一条直线，才能得结论；
先利用角平分线性质得出；再证
≌
，易证AD垂直平分EF．
由，只能得D在EF的垂直平分线上，不能说AD垂直平分EF．
是
的角平分线，
，
，
，
在
和
中，
，
≌
，
，又，
垂直平分
到线段两端点的距离相等的点一定在线段的垂直平分线上
．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图所示，∠ACD是△ABC的一个外角，CE平分∠ACD，F为CA延长线上的一点，FG∥CE，交AB于点G，若∠1＝70°，∠2＝30°，则∠3的度数为( )
A. 30° B. 40° C. 45° D. 50°
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图所示，已知A（
，y1），B（2，y2）为反比例函数y= 
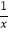图象上的两点，动点P（x，0）在x轴正半轴上运动，当线段AP与线段BP之差达到最大时，点P的坐标是（ ）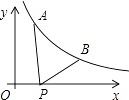
A.（ ，0）
B.（1，0）
C.（
，0）
D.（
，0） -
科目： 来源： 题型：
查看答案和解析>>【题目】已知α是锐角，且点A（
，a），B（sin30°+cos30°，b），C（﹣m2+2m﹣2，c）都在二次函数y=﹣x2+x+3的图象上，那么a、b、c的大小关系是（ ）
A.a＜b＜c
B.a＜c＜b
C.b＜c＜a
D.c＜b＜a -
科目： 来源： 题型：
查看答案和解析>>【题目】如图所示：一副三角板如图放置，等腰直角三角板ABC固定不动，另一块三角板的直角顶点放在等腰直角三角形的斜边中点D处，且可以绕点D旋转，在旋转过程中，两直角边的交点G、H始终在边AB、BC上．
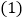在旋转过程中线段BG和CH大小有何关系？证明你的结论．
若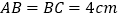
，在旋转过程中四边形GBHD的面积是否改变？若不变，求出它的值；若改变，求出它的取值范围．
若交点G、H分别在边AB、BC的延长线上，则中的结论仍然成立吗？请画出相应的图形，直接写出结论．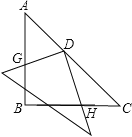
-
科目： 来源： 题型：
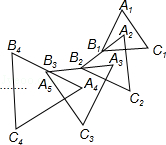
查看答案和解析>>【题目】如图，△A1B1C1是边长为1的等边三角形，A2为等边△A1B1C1的中心，连接A2B1并延长到点B2 ， 使A2B1=B1B2 ， 以A2B2为边作等边△A2B2C2 ， A3为等边△A2B2C2的中心，连接A3B2并延长到点B3 ， 使A3B2=B2B3 ， 以A3B3为边作等边△A3B3C3 ， 依次作下去得到等边△AnBnCn ， 则等边△A6B6C6的边长为 ．
-
科目： 来源： 题型：
查看答案和解析>>【题目】探索三角形的内角与外角平分线(三角形的外角是三角形的一边与另一边的延长线所组成的角)：
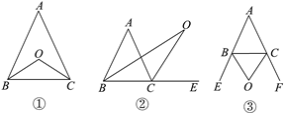
(1)如图①，在△ABC中，BO平分∠ABC，CO平分∠ACB，若∠A＝50°，则∠BOC＝________；此时∠A与∠BOC有怎样的关系？试说明理由．
(2)如图②，BO平分∠ABC，CO平分∠ACE，若∠A＝50°，则∠BOC＝________；此时∠A与∠BOC有怎样的关系？试说明理由．
(3)如图③,△ABC的外角∠CBE,∠BCF的平分线BO，CO相交于点O，若∠A＝50°,则∠BOC＝______；此时∠A与∠BOC有怎样的关系？(不需说明理由)
相关试题
