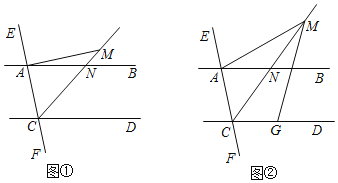
【题目】直线AB∥CD,直线EF分别交AB、CD于点A、C,CM是∠ACD的平分线,CM交AB于点N.
(1)如图①,过点A作AC的垂线交CM于点M,若∠MCD=55°,求∠MAN的度数;
(2)如图②,点G是CD上的一点,连接MA、MG,若MC平分∠AMG且∠AMG=36°,∠MGD+∠EAB=180°,求∠ACD的度数.

参考答案:
【答案】(1)∠MAN=20°;(2)∠ACD=108°.
【解析】
(1)依据角平分线的定义以及平行线的性质,即可得到∠BAC的度数,再根据垂线的定义,即可得出∠MAN的度数;
(2)设∠ACD=α,根据角平分线以及平行线即可得到∠MCG=![]() ,ACD=
,ACD=![]() α,∠BAC=∠MGD=180°-α,依据三角形外角性质,即可得到α的度数.
α,∠BAC=∠MGD=180°-α,依据三角形外角性质,即可得到α的度数.
(1)∵CM是∠ACD的平分线,∠MCD=55°,
∴∠ACD=2∠MCD=110°,
又∵AB∥CD,
∴∠BAC=180°﹣110°=70°,
又∵AM⊥EF,
∴∠MAN=90°﹣70°=20°;
(2)∵MC平分∠AMG且∠AMG=36°,
∴∠CMG=18°,
∵MC平分∠ACG,
∴∠MCG=![]() ∠ACG,
∠ACG,
∵∠CAB+∠EAB=180°,∠MGD+∠EAB=180°,
∴∠BAC=∠MGD,
∵AB∥CD,
∴∠BAC+∠ACD=180°,
设∠ACD=α,则∠MCG=![]() ACD=
ACD=![]() α,∠BAC=∠MGD=180°﹣α,
α,∠BAC=∠MGD=180°﹣α,
∵∠MGD是△CMG的外角,
∴∠MGD=∠CMG+∠MCG,即180°﹣α=![]() α+18°,
α+18°,
解得α=108°,
∴∠ACD=108°.
-
科目: 来源: 题型:
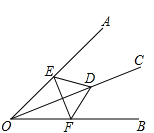
查看答案和解析>>【题目】如图,已知射线OC上的任意一点到∠AOB的两边的距离都相等,点D、E、F分别为边OC、OA、OB上,如果要想证得OE=OF,只需要添加以下四个条件中的某一个即可,请写出所有可能的条件的序号__________.
①∠ODE=∠ODF;②∠OED=∠OFD;③ED=FD;④EF⊥OC.
-
科目: 来源: 题型:
查看答案和解析>>【题目】从广州去某市,可乘坐普通列车或高铁,已知高铁的行驶路程是400千米,普通列车的行驶路程是高铁的行驶路程的1.3倍.
(1)求普通列车的行驶路程;
(2)若高铁的平均速度(千米/时)是普通列车平均速度(千米/时)的2.5倍,且乘坐高铁所需时间比乘坐普通列车所需时间缩短3小时,求高铁的平均速度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我市在创建全国文明城市过程中,决定购买A,B两种树苗对某路段道路进行绿化改造,已知购买A种树苗8棵,B种树苗3棵,需要950元;若购买A种树苗5棵,B种树苗6棵,则需要800元.
(1)求购买A,B两种树苗每棵各需多少元?
(2)考虑到绿化效果和资金周转,购进A种树苗不能少于52棵,且用于购买这两种树苗的资金不能超过7650元,若购进这两种树苗共100棵,则有哪几种购买方案?
(3)某包工队承包种植任务,若种好一棵A种树苗可获工钱30元,种好一棵B种树苗可获工钱20元,在第(2)问的各种购买方案中,种好这100棵树苗,哪一种购买方案所付的种植工钱最少?最少工钱是多少元?
-
科目: 来源: 题型:
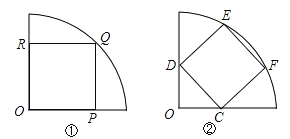
查看答案和解析>>【题目】有一批圆心角为90o,半径为3的扇形下脚料,现利用这批材料截取尽可能大的正方形材料,如图有两种截取方法:
方法一:如图1所示,正方形OPQR的顶点P、Q、R均在扇形的边界上;
方法二:如图2所示,正方形顶点C、D、E、F均在扇形边界上.
试分别求这两种截取方法得到的正方形面积,并说明哪种截取方法得到的正方形面积更大.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,△DAC、△EBC均是等边三角形,点A、C、B在同一条直线上,且AE、BD分别与CD、CE交于点M、N.

求证:(1)AE=DB;
(2)△CMN为等边三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系
 中,点
中,点 的坐标为(0,4),线段
的坐标为(0,4),线段 的位置如图所示,其中点
的位置如图所示,其中点 的坐标为(
的坐标为( ,
,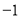 ),点
),点 的坐标为(3,
的坐标为(3, ).
).
(1)将线段
 平移得到线段
平移得到线段 ,其中点
,其中点 的对应点为
的对应点为 ,点
,点 的对应点为点
的对应点为点 .
.①点
 平移到点
平移到点 的过程可以是:先向 平移 个单位长度,再向 平移 个单位长度;
的过程可以是:先向 平移 个单位长度,再向 平移 个单位长度;②点
 的坐标为 .
的坐标为 .(2)在(1)的条件下,若点
 的坐标为(4,0),连接
的坐标为(4,0),连接 ,画出图形并求
,画出图形并求 的面积.
的面积.
相关试题

