搜索
【题目】如图，已知△ABC
（1）①用直尺和圆规作出∠ACB的角平分线CD；（不写作法，但保留作图痕迹）
②过点D画出△ADC的高DE和△DCB的高DF；
（2）量出DE，DF的长度，你有怎样的发现？并把你的发现用文字语言表达出来.
参考答案：
【答案】
（1）解：如图所示：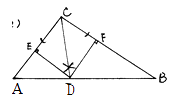
（2）解：量得 
,角平分线上的点到角两边的距离相等
【解析】（1）按要求画出图形即可。
（2）量出量出DE，DF的长度，得出结论角平分线上的点到角两边的距离相等。
【考点精析】本题主要考查了角的平分线和角平分线的性质定理的相关知识点，需要掌握从一个角的顶点引出的一条射线，把这个角分成两个相等的角，这条射线叫做这个角的平分线；定理1：在角的平分线上的点到这个角的两边的距离相等； 定理2：一个角的两边的距离相等的点，在这个角的平分线上才能正确解答此题．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图①,在△ABC中,AB=AC,点D是BC的中点,点E在AD上.
（1）求证:BE=CE.
（2）如图②,若BE的延长线交AC于点F,且BF⊥AC,垂足为F,AF=BF,原题设其他条件不变.求证:△AEF≌△BCF. -
科目： 来源： 题型：
查看答案和解析>>【题目】列方程解应用题
《九章算术》中有“盈不足术”的问题，原文如下：“今有共買羊，人出五，不足四十五；人出七，不足三.问人数、羊價各幾何？”题意是：若干人共同出资买羊，每人出5元，则差45元；每人出7元，则差3元.求人数和羊价各是多少？
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图,AB=AC,∠BAC=90°,∠1=∠2,CE⊥BE.
求证:BD=2CE.
-
科目： 来源： 题型：
查看答案和解析>>【题目】下列计算正确的是（）
A.（a3）4=a7B.a2+a2=2a4C.（-a2b3）2=a4b6D.a3÷a3=a
-
科目： 来源： 题型：
查看答案和解析>>【题目】若三角形的两条边的长度是4cm和7cm，则第三条边的长度可能是（）
A.2cmB.3cmC.8cmD.12cm
-
科目： 来源： 题型：
查看答案和解析>>【题目】问题提出：如图1，在Rt△ABC中，∠ACB=90°，CB=4，CA=6，⊙C半径为2，P为圆上一动点，连结AP、BP，求AP+
BP的最小值．（1）尝试解决：为了解决这个问题，下面给出一种解题思路：如图2，连接CP，在CB上取点D，使CD=1，则有
，又∵∠PCD=∠BCP，∴△PCD∽△BCP．∴
，∴PD=
BP，∴AP+
BP=AP+PD．请你完成余下的思考，并直接写出答案：AP+
BP的最小值为 ．（2）自主探索：在“问题提出”的条件不变的情况下，
AP+BP的最小值为 ．（3）拓展延伸：已知扇形COD中，∠COD=90°，OC=6，OA=3，OB=5，点P是
上一点，求2PA+PB的最小值．
相关试题
