【题目】如图,在三角形![]() 中,
中,![]() ,垂足为点
,垂足为点![]() ,直线
,直线![]() 过点
过点![]() ,且
,且![]() ,点
,点![]() 为线段
为线段![]() 上一点,连接
上一点,连接![]() ,∠BCG与∠BCE的角平分线CM、CN分别交
,∠BCG与∠BCE的角平分线CM、CN分别交![]() 于点M、N,若
于点M、N,若![]() ,则
,则![]() =_________°.
=_________°.

参考答案:
【答案】![]()
【解析】
依据![]() 得90°-∠B=∠BAD,已知90°-∠FCB=∠BAD,可得∠FCB=∠B,进而判定EF∥AB,即可得到∠ECG=∠BGC=70°,再根据∠MCN=∠BCN-∠BCM=
得90°-∠B=∠BAD,已知90°-∠FCB=∠BAD,可得∠FCB=∠B,进而判定EF∥AB,即可得到∠ECG=∠BGC=70°,再根据∠MCN=∠BCN-∠BCM=![]() (∠BCE-∠BCG)=
(∠BCE-∠BCG)=![]() ∠ECG,即可得到结论.
∠ECG,即可得到结论.
解:∵AD⊥BC,
∴Rt△ABD中,90°-∠B=∠BAD,
又∵90°-∠FCB=∠BAD,
∴∠FCB=∠B,
∴EF∥AB,
∴∠ECG=∠BGC=70°,
∵∠BCG与∠BCE的角平分线CM、CN分别交AD于点M、N,
∴∠BCN=![]() ∠BCE,∠BCM=
∠BCE,∠BCM=![]() ∠BCG,
∠BCG,
∴∠MCN=∠BCN-∠BCM=![]() (∠BCE-∠BCG)=
(∠BCE-∠BCG)=![]() ∠ECG,
∠ECG,
∵∠ECG=∠BGC=70°,
∴∠MCN=![]() ×70°=35°,
×70°=35°,
故答案为:35.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面材料:
小天在学习锐角三角函数中遇到这样一个问题:在Rt△ABC中,∠C=90°,∠B=22.5°,则tan22.5°=
小天根据学习几何的经验,先画出了几何图形(如图1),他发现22.5°不是特殊角,但它是特殊角45°的一半,若构造有特殊角的直角三角形,则可能解决这个问题.于是小天尝试着在CB边上截取CD=CA,连接AD(如图2),通过构造有特殊角(45°)的直角三角形,经过推理和计算使问题得到解决.
请回答:tan22.5°= .
参考小天思考问题的方法,解决问题:
如图3,在等腰△ABC 中,AB=AC,∠A=30°,请借助△ABC,构造出15°的角,并求出该角的正切值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,D是BC的中点,过D点的直线GF交AC于F,交AC的平行线BG于G点,DE⊥DF,交AB于点E,连结EG、EF.

(1)求证:BG=CF.
(2)请你判断BE+CF与EF的大小关系,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,
 为坐标原点,点
为坐标原点,点 和点
和点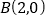 是坐标轴上两点,点
是坐标轴上两点,点 为坐标轴上一点,若三角形
为坐标轴上一点,若三角形 的面积为
的面积为 ,则
,则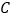 点坐标为__________.
点坐标为__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一种实验用轨道弹珠,在轨道上行驶5分钟后离开轨道,前2分钟其速度v(米/分)与时间t(分)满足二次函数v=at2,后三分钟其速度v(米/分)与时间t(分)满足反比例函数关系,如图,轨道旁边的测速仪测得弹珠1分钟末的速度为2米/分,求:
(1)二次函数和反比例函数的关系式.
(2)弹珠在轨道上行驶的最大速度.

【答案】(1)v=
 (2<t≤5) (2)8米/分
(2<t≤5) (2)8米/分【解析】分析:(1)由图象可知前一分钟过点(1,2),后三分钟时过点(2,8),分别利用待定系数法可求得函数解析式;
(2)把t=2代入(1)中二次函数解析式即可.
详解:(1)v=at2的图象经过点(1,2),
∴a=2.
∴二次函数的解析式为:v=2t2,(0≤t≤2);
设反比例函数的解析式为v=
 ,
,由题意知,图象经过点(2,8),
∴k=16,
∴反比例函数的解析式为v=
 (2<t≤5);
(2<t≤5);(2)∵二次函数v=2t2,(0≤t≤2)的图象开口向上,对称轴为y轴,
∴弹珠在轨道上行驶的最大速度在2秒末,为8米/分.
点睛:本题考查了反比例函数和二次函数的应用.解题的关键是从图中得到关键性的信息:自变量的取值范围和图象所经过的点的坐标.
【题型】解答题
【结束】
24【题目】阅读材料:小胖同学发现这样一个规律:两个顶角相等的等腰三角形,如果具有公共的顶角的顶点,并把它们的底角顶点连接起来则形成一组旋转全等的三角形.小胖把具有这个规律的图形称为“手拉手”图形.如图1,在“手拉手”图形中,小胖发现若∠BAC=∠DAE,AB=AC,AD=AE,则BD=CE.
(1)在图1中证明小胖的发现;
借助小胖同学总结规律,构造“手拉手”图形来解答下面的问题:
(2)如图2,AB=BC,∠ABC=∠BDC=60°,求证:AD+CD=BD;
(3)如图3,在△ABC中,AB=AC,∠BAC=m°,点E为△ABC外一点,点D为BC中点,∠EBC=∠ACF,ED⊥FD,求∠EAF的度数(用含有m的式子表示).

-
科目: 来源: 题型:
查看答案和解析>>【题目】寒假将近,某学校将组织七年级部分同学去亚布力参加“冰雪冬令营”.学校提前给所去学生预定房间,如果在所预定的房间里每间住
 人,则有
人,则有 人无法安排;每间住
人无法安排;每间住 人,则空出
人,则空出 张床.
张床.(1)本次参加“冰雪冬令营”的学生总数为多少人?
(2)冬令营结束时,学校准备给这些同学每人送一个售价为
 元的
元的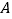 或
或 种纪念品,但实际购买时发现,
种纪念品,但实际购买时发现,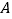 、
、 两种商品的售价都有变动,
两种商品的售价都有变动,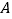 种商品打八折出售,
种商品打八折出售, 种商品的价钱比原售价提高了
种商品的价钱比原售价提高了 ,若实际购买
,若实际购买 种商品费用比购买
种商品费用比购买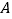 种商品费用的
种商品费用的 倍多
倍多 元,那么此次活动中学校购买
元,那么此次活动中学校购买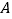 种商品多少个?
种商品多少个? -
科目: 来源: 题型:
查看答案和解析>>【题目】在正方形ABCD中,DE为正方形的外角∠ADF的角平分线,点G在线段AD上,过点G作PG⊥DE于点P,连接CP,过点D作DQ⊥PC于点Q,交射线PG于点H.

(1)如图1,若点G与点A重合.
①依题意补全图1;
②判断DH与PC的数量关系并加以证明;
(2)如图2,若点H恰好在线段AB上,正方形ABCD的边长为1,请写出求DP长的思路(可以不写出计算结果).
相关试题

