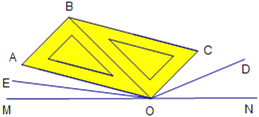
【题目】点O在直线MN上,把两个一样的三角尺按图12所示放置,OD,OE分别平分∠CON和∠AOM.
(1)若∠EOM=10°,求∠NOD的度数;
(2)求∠EOD的度数;
(3)如果保持两个三角尺拼成的图形不变,绕点O转动两个三角尺,使∠CON逐渐变小,那么(2)中的结论会改变吗?
参考答案:
【答案】(1)∠NOD=20°;(2)∠EOD=150°;(3)不改变
【解析】
(1)由图可知,∠AOM=2∠EOM,∠BOA=30°,∠BOC=90°,∠CON=2∠NOD,据此可解答;
(2)由图可知,∠EOD=∠AOC+∠AOE+∠COD;
(3) ∠EOD=∠AOC+∠AOE+∠COD,其中∠AOC的大小不变,而∠AOE+∠COD=
![]() (∠AOM+∠CON)也是不变,据此可解答.
(∠AOM+∠CON)也是不变,据此可解答.
解:(1)因为OE平分∠AOM,∠EOM=10°,所以∠AOM=2∠EOM=20°.
因为∠AOC=120°,所以∠COM=140°.
所以∠CON=180°-∠COM=180°-140°=40°.
因为OD平分∠CON,所以∠NOD=![]() ∠CON=20°.
∠CON=20°.
(2)因为∠AOC=120°,所以∠AOM+∠CON=180°-∠AOC=60°.
因为OD,OE分别平分∠CON和∠AOM,所以∠AOE+∠COD=![]() (∠AOM+∠CON)=30°.
(∠AOM+∠CON)=30°.
所以∠EOD=∠AOC+∠AOE+∠COD=120°+30°=150°.
(3)不改变.
-
科目: 来源: 题型:
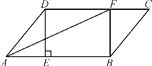
查看答案和解析>>【题目】如图,在□ABCD中,过点D作DE⊥AB于点E,点F在边CD上,CF=AE,连接AF,BF.
(1)求证:四边形BFDE是矩形
(2)若CF=6,BF=8,DF=10,求证:AF是∠DAB的平分线.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列几何体是由4个相同的小正方体搭成的,其中主视图和左视图相同的是( )

A. A B. B C. C D. D
-
科目: 来源: 题型:
查看答案和解析>>【题目】大学生小张利用暑假50天在一超市勤工俭学,被安排销售一款成本为40元/件的新型商品,此类新型商品在第x天的销售量p件与销售的天数x的关系如下表:
x(天)
1
2
3
…
50
p(件)
118
116
114
…
20
销售单价q(元/件)与x满足:当1≤x<25时q=x+60;当25≤x≤50时q=40+
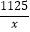 .
.
(1)请分析表格中销售量p与x的关系,求出销售量p与x的函数关系.
(2)求该超市销售该新商品第x天获得的利润y元关于x的函数关系式.
(3)这50天中,该超市第几天获得利润最大?最大利润为多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,AB=4cm,BC=8cm,动点M从点D出发,按折线DCBAD方向以2cm/s的速度运动,动点N从点D出发,按折线DABCD方向以1cm/s的速度运动。
(1)若动点M、N同时出发,经过几秒钟两点相遇?
(2)若点E在线段BC上,且BE=3cm,若动点M、N同时出发,相遇时停止运动,经过几秒钟,点A、E、M、N组成平行四边形?

-
科目: 来源: 题型:
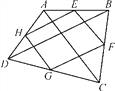
查看答案和解析>>【题目】如图所示,E,F,G,H分别是四边形ABCD的边AB,BC,CD,AD的中点.
(1)当四边形ABCD是矩形时,四边形EFGH是_________,请说明理由;
(2)当四边形ABCD满足什么条件时,四边形EFGH为正方形?并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,点C,D是半圆O的三等分点,过点C作⊙O的切线交AD的延长线于点E,过点D作DF⊥AB于点F,交⊙O于点H,连接DC,AC.
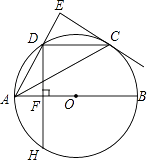
(1)求证:∠AEC=90°;
(2)试判断以点A,O,C,D为顶点的四边形的形状,并说明理由;
(3)若DC=2,求DH的长.
相关试题

