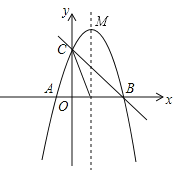
【题目】如图,已知抛物线![]() 与
与![]() 轴交于点
轴交于点![]() .
.
(1)求该抛物线的表达式;
(2)点![]() 是线段
是线段![]() 上方的抛物线上一个动点,求
上方的抛物线上一个动点,求![]() 的面积的最大值;
的面积的最大值;
(3)点![]() 是抛物线的对称轴上一个动点,当以
是抛物线的对称轴上一个动点,当以![]()
![]()
![]() 为顶点的三角形是直角三角形时,求出点
为顶点的三角形是直角三角形时,求出点![]() 的坐标.
的坐标.
参考答案:
【答案】(1)![]() ;(2)△BEC的面积的最大值为
;(2)△BEC的面积的最大值为![]() ;(3)符合条件的点
;(3)符合条件的点![]() 的坐标是
的坐标是![]() 或
或![]() 或
或![]() 或
或![]() .
.
【解析】
(1)将点A、B的坐标代入函数解析式,列出方程组,通过解方程组求得a、b的值即可;
(2)利用待定系数法确定直线BC解析式,由函数图象上点的坐标特征求得点E、F的坐标,然后根据两点间的距离公式求得EF长度,结合三角形的面积公式列出函数式,根据二次函数最值的求法求得点E的横坐标,易得其纵坐标,则点E的坐标迎刃而解了;
(3)需要分类讨论:点A、P、C分别为直角顶点,利用勾股定理求得答案.
(1)∵抛物线![]() 与
与![]() 轴交于点
轴交于点![]() ,
,
![]() ,解得
,解得![]() ,
,
![]() ;
;
(2)如图,作![]() 轴交
轴交![]() 于点
于点![]() 记
记![]() 的面积为
的面积为![]() ,
,

设直线BC的解析式为y=kx+b,
![]() ,
,
∴![]() ,
,
解得![]() ,
,
![]() 直线
直线![]() 解析式为:
解析式为:![]() .
.
设![]() ,则
,则![]() ,
,
![]() ,
,
![]() ,
,
当![]() 时,
时,![]() ,
,
此时,点![]() 的坐标是
的坐标是![]() ;
;
![]() 设
设![]() ,
,
![]() ;
;
![]() 当
当![]() 时,
时,![]()
即![]() .解得
.解得![]() ;
;
![]() 当
当![]() 时,
时,![]() ,
,
即![]() ,解得
,解得![]() ;
;
![]() 当
当![]() 时,
时,![]()
即![]() .解得
.解得![]() 或
或![]() .
.
综上所述,符合条件的点![]() 的坐标是
的坐标是![]() 或
或![]() 或
或![]() 或
或![]()
-
科目: 来源: 题型:
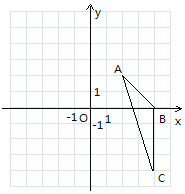
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知△ABC三个顶点的坐标分别为A(2,2),B(4,0),C(4,-4).
(1)请在图中画出△ABC向左平移6个单位长度后得到的△A1B1C1;
(2)以点O为位似中心,将△ABC缩小为原来的
 ,得到△A2B2C2,请在图中y轴右侧画出△A2B2C2,;
,得到△A2B2C2,请在图中y轴右侧画出△A2B2C2,;(3)填空:△AA1A2的面积为________________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在兰州市开展的“体育、艺术2+1”活动中,某校根据实际情况,决定主要开设A:乒
乓球,B:篮球,C:跑步,D:跳绳这四种运动项目.为了解学生喜欢哪一种项目,随机抽取了部分学生进行调查,并将调查结果绘制成如下的条形统计图和扇形统计图.请你结合图中信息解答下列问题:
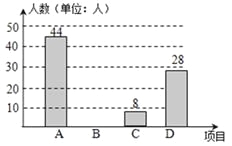
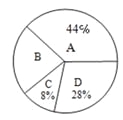
(1)样本中喜欢B项目的人数百分比是 ,其所在扇形统计图中的圆心角的度数是 ;
(2)把条形统计图补充完整;
(3)已知该校有1000人,根据样本估计全校喜欢乒乓球的人数是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某建设工程队计划每小时挖掘土石方
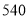 方,现决定租用甲、乙两种型号的挖掘机来完成这项工作,已知一台甲型挖掘机与一台乙型挖掘机每小时共挖土
方,现决定租用甲、乙两种型号的挖掘机来完成这项工作,已知一台甲型挖掘机与一台乙型挖掘机每小时共挖土 方,
方,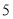 台甲型挖掘机与
台甲型挖掘机与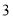 台乙型挖掘机恰好能完成每小时的挖掘量.
台乙型挖掘机恰好能完成每小时的挖掘量.(1)求甲、乙两种型号的挖掘机每小时各挖土多少方?
(2)若租用一台甲型挖掘机每小时
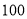 元,租用一台乙型挖掘机每小时
元,租用一台乙型挖掘机每小时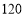 元,且每小时支付的总租金不超过
元,且每小时支付的总租金不超过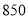 元,又恰好完成每小时的挖掘量,请设计该工程队的租用方案.
元,又恰好完成每小时的挖掘量,请设计该工程队的租用方案. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在△ABC中,AB=BC=5,AC=6.△ECD是△ABC沿BC方向平移得到的,连接AE.AC和BE相交于点O.
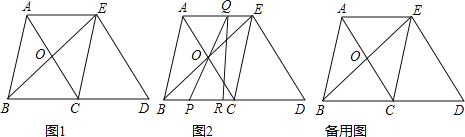
(1)判断四边形ABCE是怎样的四边形,说明理由;
(2)如图2,P是线段BC上一动点(图2),(不与点B、C重合),连接PO并延长交线段AE于点Q,QR⊥BD,垂足为点R.
①四边形PQED的面积是否随点P的运动而发生变化.若变化,请说明理由;若不变,求出四边形PQED的面积;
②当线段PB的长为何值时,△PQR与△BOC相似.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数
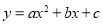 的图像如图所示,对称轴为直线
的图像如图所示,对称轴为直线 ,则下列结论正确的有( )
,则下列结论正确的有( )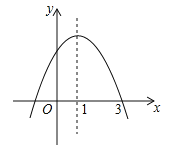
①
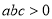 ;②方程
;②方程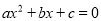 的两个根是
的两个根是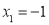 ,
,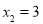 ;
;③
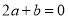 ;④当
;④当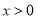 时,
时,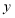 随
随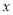 的增大而减小.
的增大而减小.A.①②B.②③C.①④D.②④
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司计划购买A,B两种型号的机器人搬运材料.已知A型机器人比B型机器人每小时多搬运30kg材料,且A型机器人搬运1000kg材料所用的时间与B型机器人搬运800kg材料所用的时间相同.
(1)求A,B两种型号的机器人每小时分别搬运多少材料;
(2)该公司计划采购A,B两种型号的机器人共20台,要求每小时搬运材料不得少于2800kg,则至少购进A型机器人多少台?
相关试题

