【题目】若xm+n=12,xn=3,(x≠0),求x2m+n的值.
参考答案:
【答案】解:∵xm+n=12,xn=3,
∴xm=xm+n﹣n=xm+n÷xn=12÷3=4.
∴x2m+n=xm+n×xm=12×4=48.
【解析】根据幂的乘方,底数不变指数相乘,先把xm和xn的值求出,然后根据同底数幂的除法,底数不变指数相减求解即可.
【考点精析】本题主要考查了同底数幂的乘法的相关知识点,需要掌握同底数幂的乘法法则aman=am+n(m,n都是正数)才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠BAC=90°,AB=AC,D点在AC上,E点在BA的延长线上,BD=CE,BD的延长线交CE于F.证明:
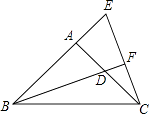
(1)AD=AE
(2)BF⊥CE. -
科目: 来源: 题型:
查看答案和解析>>【题目】某超市销售甲、乙两种糖果,购买3千克甲种糖果和1千克乙种糖果共需44元,购买1千克甲种糖果和2千克乙种糖果共需38元.
(1)求甲、乙两种糖果的价格;
(2)若购买甲、乙两种糖果共20千克,且总价不超过240元,问甲种糖果最少购买多少千克?
-
科目: 来源: 题型:
查看答案和解析>>【题目】方程(x+1)(x﹣2)=0的解是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为解决中小学大班额问题,东营市各县区今年将改扩建部分中小学,某县计划对A、B两类学校进行改扩建,根据预算,改扩建2所A类学校和3所B类学校共需资金7800万元,改扩建3所A类学校和1所B类学校共需资金5400万元.
(1)改扩建1所A类学校和1所B类学校所需资金分别是多少万元?
(2)该县计划改扩建A、B两类学校共10所,改扩建资金由国家财政和地方财政共同承担.若国家财政拨付资金不超过11800万元;地方财政投入资金不少于4000万元,其中地方财政投入到A、B两类学校的改扩建资金分别为每所300万元和500万元.请问共有哪几种改扩建方案?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知如图,在数轴上点
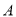 ,
, 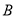 所对应的数是
所对应的数是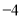 ,
, 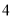 .
.对于关于
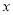 的代数式
的代数式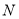 ,我们规定:当有理数
,我们规定:当有理数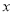 在数轴上所对应的点为
在数轴上所对应的点为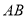 之间(包括点
之间(包括点 ,
, 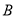 )的任意一点时,代数式
)的任意一点时,代数式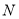 取得所有值的最大值小于等于
取得所有值的最大值小于等于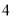 ,最小值大于等于
,最小值大于等于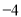 ,则称代数式
,则称代数式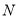 ,是线段
,是线段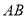 的封闭代数式.
的封闭代数式.例如,对于关于
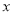 的代数式
的代数式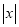 ,当
,当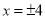 时,代数式
时,代数式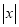 取得最大值是
取得最大值是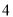 ;当
;当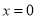 时,代数式
时,代数式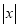 取得最小值是
取得最小值是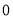 ,所以代数式
,所以代数式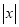 是线段
是线段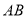 的封闭代数式.
的封闭代数式.问题:(
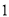 )关于
)关于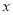 代数式
代数式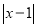 ,当有理数
,当有理数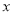 在数轴上所对应的点为
在数轴上所对应的点为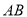 之间(包括点
之间(包括点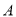 ,
, 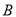 )的任意一点时,取得的最大值和最小值分别是__________.
)的任意一点时,取得的最大值和最小值分别是__________.所以代数式
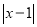 __________(填是或不是)线段
__________(填是或不是)线段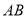 的封闭代数式.
的封闭代数式.(
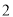 )以下关
)以下关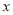 的代数式:
的代数式:①
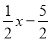 ;②
;②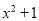 ;③
;③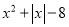 ;④
;④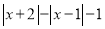 .
.是线段
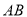 的封闭代数式是__________,并证明(只需要证明是线段
的封闭代数式是__________,并证明(只需要证明是线段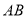 的封闭代数式的式子,不是的不需证明).
的封闭代数式的式子,不是的不需证明).(
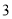 )关于
)关于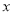 的代数式
的代数式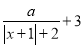 是线段
是线段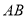 的封闭代数式,则有理数
的封闭代数式,则有理数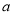 的最大值是__________,最小值是__________.
的最大值是__________,最小值是__________.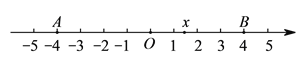
-
科目: 来源: 题型:
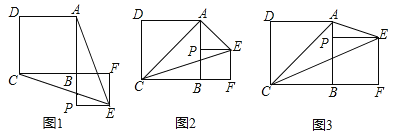
查看答案和解析>>【题目】已知正方形ABCD,P为射线AB上的一点,以BP为边作正方形BPEF,使点F在线段CB的延长线上,连接EA、EC.
(1)如图1,若点P在线段AB的延长线上,求证:EA=EC;
(2)若点P在线段AB上.
①如图2,连接AC,当P为AB的中点时,判断△ACE的形状,并说明理由;
②如图3,设AB=a,BP=b,当EP平分∠AEC时,求a:b及∠AEC的度数.
相关试题

