Question

【题目】如图，∠BAC=90°，AB=AC，D点在AC上，E点在BA的延长线上，BD=CE，BD的延长线交CE于F．证明：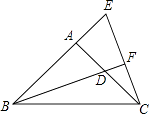

（1）AD=AE
（2）BF⊥CE．

Answer 1

【答案】
（1）证明：∵∠BAC=90°，

∴∠CAE=∠BAC=90°，

在Rt△BAD和Rt△CAE中

∴Rt△BAD≌Rt△CAE（HL），

∴AD=AE

（2）证明：由（1）可知Rt△BAD≌Rt△CAE，

∴∠ADB=∠E，

∵∠ABD+∠ADB=90°，

∴∠ABD+∠E=90°，

∴∠BFE=90°，即BF⊥CE．

【解析】（1）可证明Rt△BAD≌Rt△CAE，可证得AD=AE；（2）利用（1）中的全等，可知∠E=∠ADB，结合条件可求得∠ABD+∠E=90°，可证明BF⊥CE．