【题目】根据题意解答 
(1)感知:如图①,在△ABC中,AD平分∠BAC,AE⊥BC,∠B=40°,∠C=70°,求∠DAE度数;
(2)探究:如图②,在△ABC中,若把“AE⊥BC”变成“点F在DA的延长线上,FE⊥BC,其他条件不变,求∠DFE的度数”;
(3)拓展:如图③,若把△ABC变成四边形ABEC,把AE⊥BC变成EA平分∠BEC,其他条件不变,∠DAE的度数是否变化,并且说明理由.
参考答案:
【答案】
(1)解:∵∠B=40°,∠C=70°,
∴∠BAC=70°,
∵AD平分∠BAC,
∴∠BAD=∠CAD=35°,
∴∠ADE=∠B+∠BAD=75°,
∵AE⊥BC,
∴∠AEB=90°,
∴∠DAE=90°﹣∠ADE=15°.
(2)解:同(1),可得,∠ADE=75°,
∵FE⊥BC,
∴∠FEB=90°,
∴∠DFE=90°﹣∠ADE=15°.
(3)解:结论:∠DAE的度数大小不变.
证明:∵AE平分∠BEC,
∴∠AEB=∠AEC,
∴∠C+∠CAE=∠B+∠BAE,
∵∠CAE=∠CAD﹣∠DAE,∠BAE=∠BAD+∠DAE,
∴∠C+∠CAD﹣∠DAE=∠B+∠BAD+∠DAE,
∵AD平分∠BAC,
∴∠BAD=∠CAD,
∴2∠DAE=∠C﹣∠B=30°,
∴∠DAE=15°.
【解析】(1)求出∠ADE的度数,利用∠DAE=90°﹣∠ADE即可求出∠DAE的度数.(2)求出∠ADE的度数,利用∠DFE=90°﹣∠ADE即可求出∠DAE的度数.(3)利用AE平分∠BEC,AD平分∠BAC,求出∠DFE=15°即是最好的证明.
【考点精析】解答此题的关键在于理解三角形的内角和外角的相关知识,掌握三角形的三个内角中,只可能有一个内角是直角或钝角;直角三角形的两个锐角互余;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角.
-
科目: 来源: 题型:
查看答案和解析>>【题目】国际奥委会会旗上的五环图案可以看作一个基本图案圆环经过______运动得到
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知E,F分别为正方形ABCD的边BC,CD上的点,AF,DE相交于点G,当E,F分别为边BC,CD的中点时,有:①AF=DE;②AF⊥DE成立.
试探究下列问题:
(1)如图1,若点E不是边BC的中点,F不是边CD的中点,且CE=DF,上述结论①,②是否仍然成立?(请直接回答“成立”或“不成立”),不需要证明)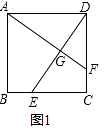
(2)如图2,若点E,F分别在CB的延长线和DC的延长线上,且CE=DF,此时,上述结论①,②是否仍然成立?若成立,请写出证明过程,若不成立,请说明理由;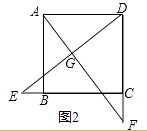
(3)如图3,在(2)的基础上,连接AE和EF,若点M,N,P,Q分别为AE,EF,FD,AD的中点,请判断四边形MNPQ是“矩形、菱形、正方形”中的哪一种,并证明你的结论.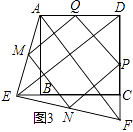
-
科目: 来源: 题型:
查看答案和解析>>【题目】一件夹克衫先按成本提高50%标价,再以8折(标价的80%)出售,结果获利20元,若设这件夹克衫的成本是x元,根据题意,可得到的方程是( )
A.(1+50%)x×80%=x﹣20
B.(1+50%)x×80%=x+20
C.(1+50%x)×80%=x﹣20
D.(1+50%x)×80%=x+20 -
科目: 来源: 题型:
查看答案和解析>>【题目】以下列线段为边,能组成直角三角形的是( )
A.6cm,12cm,14cm
B. cm,1cm,
cm,1cm,  cm
cm
C.1.5cm,2cm,2.5cm
D.2cm,3cm,5cm -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,延长AB至E,延长CD至F,BE=DF,连接EF,与BC、AD分别相交于P、Q两点.
(1)求证:CP=AQ;
(2)若BP=1,PQ=
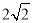 ,∠AEF=45°,求矩形ABCD的面积.
,∠AEF=45°,求矩形ABCD的面积.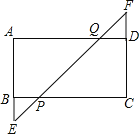
-
科目: 来源: 题型:
查看答案和解析>>【题目】若(n+3)2n的值为1,则n的值为_____.
相关试题

