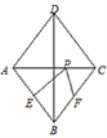
【题目】如图,在菱形ABCD中,对角线AC=6,BD=8,点E、F分别是边AB、BC的中点,点P在AC上运动,在运动过程中,存在PE+PF的最小值,则这个最小值是________________
参考答案:
【答案】5
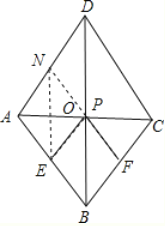
【解析】试题分析:AC交BD于O,作E关于AC的对称点N,连接NF,交AC于P,则此时EP+FP的值最小,
∴PN=PE, ∵四边形ABCD是菱形, ∴∠DAB=∠BCD,AD=AB=BC=CD,OA=OC,OB=OD,AD∥BC,
∵E为AB的中点, ∴N在AD上,且N为AD的中点, ∵AD∥CB, ∴∠ANP=∠CFP,∠NAP=∠FCP,
∵AD=BC,N为AD中点,F为BC中点, ∴AN=CF, ∴△ANP≌△CFP(ASA), ∴AP=CP,
即P为AC中点, ∵O为AC中点, ∴P、O重合, 即NF过O点, ∵AN∥BF,AN=BF,
∴四边形ANFB是平行四边形, ∴NF=AB, ∵菱形ABCD,
∴AC⊥BD,OA=![]() AC=3,BO=
AC=3,BO=![]() BD=4,由勾股定理得:AB=5,
BD=4,由勾股定理得:AB=5,
-
科目: 来源: 题型:
查看答案和解析>>【题目】小颖和小红两位同学在学习“概率”时,做投掷骰子(质地均匀的正方体)实验,他们共做了60次实验,实验的结果如下:
朝上的点数
1
2
3
4
5
6
出现的次数
7
9
6
8
20
10
(1)计算“3点朝上”的频率和“5点朝上”的频率;
(2)小颖说:“根据上述实验,一次实验中出现5点朝上的概率最大”;小红说:“如果投掷600次,那么出现6点朝上的次数正好是100次”,小颖和小红的说法正确吗?为什么?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中有两点A(-2,2),B(1,4),根据要求求出P点的坐标:
(1)在x轴上找一点P,使得
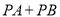 最小
最小(2)在y轴上找一点P,使得
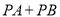 最小
最小(3)在x轴上找一点P,使得
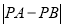 最大
最大(4)在x轴上找一点P,使得
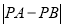 最小
最小 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图□ABCD的对角线AC、BD交于点O ,AE平分∠BAD交BC于点E ,且∠ADC=600,AB=
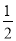 BC ,连接OE .下列 结论:①∠CAD=300 ② S□ABCD=ABAC ③ OB=AB ④ OE=
BC ,连接OE .下列 结论:①∠CAD=300 ② S□ABCD=ABAC ③ OB=AB ④ OE=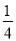 BC 成立的个数有( )
BC 成立的个数有( )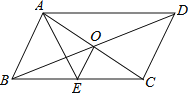
A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算正确的是( )
A. x2x4=x8 B. 5×59=50 C. (﹣a)2a5=a7 D. (﹣a)a6=﹣a6
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线y=kx+b与x轴的交点坐标是(2,0),则关于x的方程kx+b=0的解是x=______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:(﹣2ab2)3÷4a2b2=_____.
相关试题

