【题目】方成同学看到一则材料,甲开汽车,乙骑自行车从M地出发沿一条公路匀速前往N地,设乙行驶的时间为t(h),甲乙两人之间的距离为y(km),y与t的函数关系如图1所示,方成思考后发现了图1的部分正确信息,乙先出发1h,甲出发20分钟后与乙相遇,…,请你帮助方成同学解决以下问题: 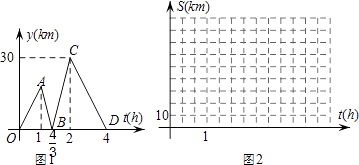
(1)分别求出线段BC,CD所在直线的函数表达式;
(2)当15<y<25时,求t的取值范围;
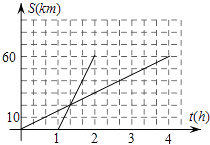
(3)分别求出甲、乙行驶的路程S甲、S乙与时间t的函数表达式,并在图2所给的直角坐标系中分别画出它们的图象.
参考答案:
【答案】
(1)解:设线段BC所在直线的函数表达式为y=k1t+b1,
将点B( ![]() ,0),点C(2,30)代入函数解析式,得
,0),点C(2,30)代入函数解析式,得
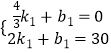 ,解得:
,解得: ![]() .
.
故线段BC所在直线的函数表达式为y=45t﹣60( ![]() ≤t≤2).
≤t≤2).
设线段CD所在直线的函数表达式为y=k2t+b2,
将点C(2,30),点D(4,0)代入函数解析式,得
![]() ,解得:
,解得: ![]() .
.
故线段CD所在直线的函数表达式为y=﹣15t+60(2<t≤4)
(2)解:乙骑车的速度为30÷(4﹣2)=15(km/h),
∴线段OA所在直线的函数表达式为y=15t(0≤t≤1),
∴点A的纵坐标为15.
当15<y<25时,即15<45t﹣60<25或15<﹣15t+60<25,
解得: ![]() <t<
<t< ![]() 或
或 ![]() <t<3.
<t<3.
故当15<y<25时,t的取值范围为 ![]() <t<
<t< ![]() 或
或 ![]() <t<3
<t<3
(3)解:甲开车的速度15÷( ![]() ﹣1)+15=60(km/h),
﹣1)+15=60(km/h),
∴S甲=60(t﹣1)=60t﹣60(1≤t≤2),S乙=15t(0≤t≤4).
所画图形如图.
【解析】(1)设线段BC所在直线的函数表达式为y=k1t+b1 , 将点B、C的坐标代入其中得出关于k1、b1的二元一次方程组,解方程组即可求出结论;设线段CD所在直线的函数表达式为y=k2t+b2 , 将点C、D的坐标代入其中得出关于k2、b2的二元一次方程组,解方程组即可得出结论;(2)根据线段CD可求出乙骑车的速度,从而得出线段OA的函数解析式,结合题意列出关于t的一元一次不等式,解不等式即可得出结论;(3)根据图象求出甲开车的速度,由路程=速度×时间得出S甲、S乙与时间t的函数表达式,画出图形即可.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为增强学生的身体素质,教育行政部门规定学生每天参加户外活动的平均时间不少于1小时.为了解学生参加户外活动的情况,对部分学生参加户外活动的时间进行抽样调查,并将调查结果绘制作成如下两幅不完整的统计图,请你根据图中提供的信息解答下列问题:
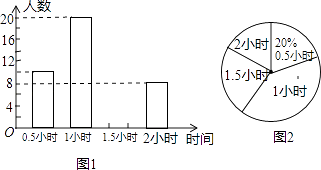
(1)一共调查了多少名学生;
(2)请补全条形统计图;
(3)若该校共有6000名学生,根据以上调查结果估计该校全体学生每天参与户外活动所用的总时间. -
科目: 来源: 题型:
查看答案和解析>>【题目】某厂家新开发的一种摩托车如图所示,它的大灯A射出的光线AB、AC与地面MN的夹角分别为8°和10°,大灯A离地面距离1m.

(1)该车大灯照亮地面的宽度BC约是多少(不考虑其它因素)?
(2)一般正常人从发现危险到做出刹车动作的反应时间是0.2s,从发现危险到摩托车完全停下所行驶的距离叫做最小安全距离,某人以60km/h的速度驾驶该车,从60km/h到摩托车停止的刹车距离是 m,请判断该车大灯的设计是否能满足最小安全距离的要求,请说明理由.参考数据:sin8°≈
m,请判断该车大灯的设计是否能满足最小安全距离的要求,请说明理由.参考数据:sin8°≈  ,tan8°≈
,tan8°≈  ,sin10°≈
,sin10°≈  ,tan10°≈
,tan10°≈  .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,直线l:y1=2x+4,与y轴交于点A,与x轴交于点B,反比例函数y2=
 与直线l交于点C,且AB=2AC.
与直线l交于点C,且AB=2AC. 
(1)求反比例函数的解析式;
(2)根据函数图象,直接写出0<y1<y2的x的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】定义{a,b,c}为函数y=ax2+bx+c的“特征数”.
(1)“特征数”为{﹣1,2,3}的函数解析式为 , 将“特征数”为{0,1,1}的函数向下平移两个单位以后得到的函数解析式为;
(2)我们把横、纵坐标均为整数的点称为“整点”,试问:在上述两空填写的函数图象围成的封闭图形(包含边界)内共有多少个整点?请给出详细的运算过程;
(3)定义“特征数”的运算:①{a1 , b1 , c1}+{a2 , b2 , c2}={a1+a2 , b1+b2 , c1+c2};②λ{a1 , b1 , c1}={λa1 , λb1 , λc1}(其中λ为任意常数).试问:“特征数”为{﹣1,2,3}+λ{0,1,﹣1}的函数是否过定点?如果过定点,请计算出该定点坐标;如果不存在,请说明你的理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,ABCD为正方形,直线MN分别过AD边与BC边的中点,点P为直线MN上任意一点,连接PB、PC分别与AD边交于E、F两点,PC与BD交于点K,连接AK与PB交于点G.
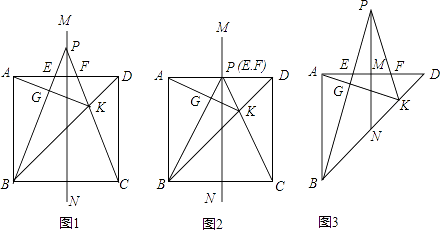
(1)探索发现
当点P落在AD边上时,如图2,试探究PB与AK的位置关系以及PB、PK、AK三者的数量关系(直接写出无需证明);
(2)延伸拓展
当点P落在正方形外,如图1,以上两个结论是否仍然成立?如果成立请给出证明,如果不成立请说明你的理由;
(3)应用推广
如图3,在等腰Rt△ABD中,其中∠BAD=90°,腰长为3,M、N分别为AD边与BD边的中点,K为线段DN中点,F为AD边上靠近于D的三等分点.连接KF并延长与直线MN交于点P,连接PB分别与AD、AK交于点E、G.试求四边形EFKG的周长及面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】将边长为2的正方形OABC如图放置,O为原点.若∠α=15°,则点B的坐标为 .

相关试题

