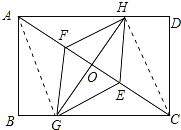
【题目】四边形ABCD 中,AB=3,BC=4,E,F 是对角线 AC上的两个动点,分别从 A,C 同时出发, 相向而行,速度均为 1cm/s,运动时间为 t 秒,当其中一个动点到达后就停止运动.
(1)若 G,H 分别是 AB,DC 中点,求证:四边形 EGFH 始终是平行四边形.
(2)在(1)条件下,当 t 为何值时,四边形 EGFH 为矩形.
(3)若 G,H 分别是折线 A﹣B﹣C,C﹣D﹣A 上的动点,与 E,F 相同的速度同时出发,当 t 为何值时,四边形 EGFH 为菱形.

参考答案:
【答案】(1)证明见解析;
(2)当 t 为0.5s或4.5s时,四边形 EGFH 为矩形;
(3)t为![]() s时,四边形EGFH为菱形.
s时,四边形EGFH为菱形.
【解析】试题分析:(1)由矩形的性质得出AB=CD,AB∥CD,AD∥BC,∠B=90°,由勾股定理求出AC=5,由SAS证明△AFG≌△CEH,得出GF=HE,同理得出GE=HF,即可得出结论;
(2)先证明四边形BCHG是平行四边形,得出GH=BC=4,当对角线EF=GH=4时,平行四边形EGFH是矩形,分两种情况:①AE=CF=t,得出EF=5-2t=4,解方程即可;②AE=CF=t,得出EF=5-2(5-t)=4,解方程即可;
(3)连接AG、CH,由菱形的性质得出GH⊥EF,OG=OH,OE=OF,得出OA=OC,AG=AH,证出四边形AGCH是菱形,得出AG=CG,设AG=CG=x,则BG=4-x,由勾股定理得出方程,解方程求出BG,得出AB+BG=![]() ,即可得出t的值.
,即可得出t的值.
试题解析:(1)∵四边形ABCD是矩形,
∴AB=CD,AB∥CD,AD∥BC,∠B=90°,
∴AC=![]() =5,∠GAF=∠HCE,
=5,∠GAF=∠HCE,
∵G,H分别是AB,DC中点,
∴AG=BG,CH=DH,
∴AG=CH,
∵AE=CF,
在△AFG和△CEH中,
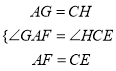
∴△AFG≌△CEH(SAS),
∴GF=HE,
同理:GE=HF,
∴四边形EGFH是平行四边形.
(2)由(1)得:BG=CH,BG∥CH,
∴四边形BCHG是平行四边形,
∴GH=BC=4,当EF=GH=4时,平行四边形EGFH是矩形,分两种情况:
①AE=CF=t,EF=5﹣2t=4,解得:t=0.5;
②AE=CF=t,EF=5﹣2(5﹣t)=4,解得:t=4.5;
综上所述:当t为0.5s或4.5s时,四边形EGFH为矩形.
(3)连接AG、CH,如图所示:
∵四边形EGFH为菱形,
∴GH⊥EF,OG=OH,OE=OF,
∴OA=OC,AG=AH,
∴四边形AGCH是菱形,
∴AG=CG,
设AG=CG=x,则BG=4﹣x,由勾股定理得:AB2+BG2=AG2,即32+(4﹣x)2=x2,
解得:x=![]() ,
,
∴BG=4﹣![]() =
=![]() ,
,
∴AB+BG=3+![]() =
=![]() ,
,
即t为![]() s时,四边形EGFH为菱形.
s时,四边形EGFH为菱形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果点A(1,m)在直线y=-2x+1上,那么m=___________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,①②③④⑤五个平行四边形拼成一个含30度内角的菱形EFGH(不重叠无缝隙).若①②③④四个平行四边形面积的和为26cm2,四边形ABCD面积是19cm2,则①②③④四个平行四边形周长的总和为( )

A. 96cm B. 64cm C. 48cm D. 36cm
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知Rt△ABC中,∠ACB=90°,以斜边AB为边向外作正方形ABDE,且正方形的对角线交于点O,连结OC.已知AC=5,OC=6
 ,则另一直角边BC的长为 .
,则另一直角边BC的长为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,B为线段AD上一点,△ABC和△BDE都是等边三角形,连接CE并延长,交AD的延长线于F,△ABC的外接圆⊙O交CF于点M.

(1)求证:BE是⊙O的切线;
(2)求证:AC2=CMCF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学九(1)班为了了解全班学生喜欢球类活动的情况,采取全面调查的方法,从足球、乒乓球、篮球、排球等四个方面调查了全班学生的兴趣爱好,根据调查的结果组建了4个兴趣小组,并绘制成如图所示的两幅不完整的统计图(如图①,②,要求每位学生只能选择一种自己喜欢的球类),请你根据图中提供的信息解答下列问题:
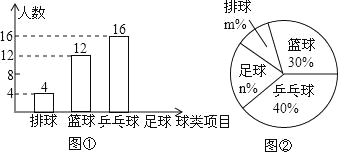
(1)九(1)班的学生人数为 ,并把条形统计图补充完整;
(2)扇形统计图中m= ,n= ,表示“足球”的扇形的圆心角是 度;
(3)排球兴趣小组4名学生中有3男1女,现在打算从中随机选出2名学生参加学校的排球队,请用列表或画树状图的方法求选出的2名学生恰好是1男1女的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知两个有理数的和比其中任何一个加数都小 ,那么一定是 ( )
A. 这两个有理数同为正数 B. 这两个有理数同为负数
C. 这两个有理数异号 D. 这两个有理数中有一个为零
相关试题

