【题目】如图,l1∥l2,MN分别和直线l1,l2交于点A,B,ME分别和直线l1,l2交于点C,D,点P在MN上(P与A,B,M三点不重合)
①如果点P在A,B两点之间运动时,∠α,∠β,∠γ之间有何数量关系?请说明理由.
②如果点P在A,B两点外运动时,∠α,∠β,∠γ之间有何数量关系?


参考答案:
【答案】(1)∠γ=∠α+∠β (2)∠β=∠α+∠γ ∠α=∠β+∠γ
【解析】(1)根据平行线的性质可求出它们的关系,从点P作平行线,平行于AC,根据两直线平行内错角相等可得出;
(2)分类讨论,①点P在点AB延长线上时,②点P在BA延长线上时,分别过点P作PO∥l1∥l2,利用平行线的性质,可得出答案.
(1)如图,过点P作PO∥AC,则PO∥l1∥l2,如图所示:
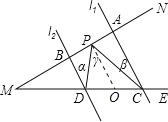
∴∠α=∠DPO,∠β=∠CPO,
∴∠γ=∠α+∠β;
(2)①若点P在BA延长线上,过点P作PO∥AC,则PO∥l1∥l2,如图所示:
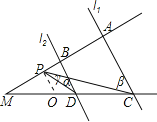
则∠β=∠α+∠γ.
②若点P在BA延长线上,过点P作PO∥AC,则PO∥l1∥l2,如图所示:
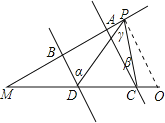
则∠α=∠β+∠γ.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在义乌中小学生“我的中国梦”读书活动中,某校对部分学生作了一次主题为“我最喜爱的图书”的调查活动,将图书分为甲、乙、丙、丁四类,学生可根据自己的爱好任选其中一类。学校根据调查情况进行了统计,并绘制了不完整的条形统计图和扇形统计图如图。
“我最喜爱的图书”各类人数统计图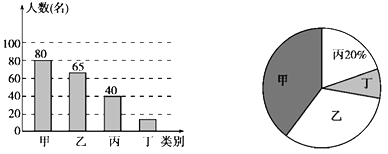
请你结合图中信息,解答下列问题:
(1)本次共调查了 名学生;
(2)被调查的学生中,最喜爱丁类图书的有 名,最喜爱甲类图书的人数占本次被调查人数的 %;
(3)在最喜爱丙类图书的学生中,女生人数是男生人数的1.5倍,若这所学校共有学生1500名,请你估计该校最喜爱丙类图书的女生和男生分别有多少名? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,AB=3,BC=5,点P是BC边上的一个动点(点P不与点B,C重合),现将△PCD沿直线PD折叠,使点C落下点C1处;作∠BPC1的平分线交AB于点E.设BP=x,BE=y,那么y关于x的函数图象大致应为( )

A.
B.
C.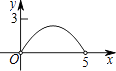
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】列方程解应用题:
为了提高产品的附加值,某公司计划将研发生产的1200件新产品进行精加工后再投放市场.现有甲、乙两个工厂都具备加工能力,公司派出相关人员分别到这两个工厂了解情况,获得如下信息:
信息一:甲工厂单独加工完成这批产品比乙工厂单独加工完成这批产品多用10天;
信息二:乙工厂每天加工的数量是甲工厂每天加工数量的1.5倍.
根据以上信息,求甲、乙两个工厂每天分别能加工多少件新产品.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图1,线段AB、CD相交于点O,连接AD、CB,我们把形如图1的图形称之为“8字形”.试解答下列问题:

(1)在图1中,请直接写出∠A、∠B、∠C、∠D之间的数量关系: ;
(2)仔细观察,在图2中“8字形”的个数: 个;
(3)在图2中,若∠D=40°,∠B=36°,∠DAB和∠BCD的平分线AP和CP相交于点P,并且与CD、AB分别相交于M、N.利用(1)的结论,试求∠P的度数;
(4)如果图2中∠D和∠B为任意角时,其他条件不变,试问∠P与∠D、∠B之间存在着怎样的数量关系.(直接写出结论即可)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,数学兴趣小组想测量电线杆AB的高度,他们发现电线杆的影子恰好落在土坡的坡面CD和地面BC上,量得CD=4米,BC=10米,CD与地面成30°角,且此时测得1米杆的影长为2米,则电线杆的高度约为米(结果保留根号)

-
科目: 来源: 题型:
查看答案和解析>>【题目】小明解方程
 -
- =1的过程如下:
=1的过程如下:解:方程两边乘x,得1-(x-2)=1.①
去括号,得1-x-2=1.②
移项,得-x=1-1+2.③
合并同类项,得-x=2.④
解得x=-2.⑤
所以,原分式方程的解为x=-2.⑥
请指出他解答过程中的错误,并写出正确的解答过程.
相关试题

