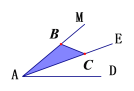
【题目】(1)如图,AE是∠MAD的平分线,点C是AE上一点,点B是AM上一点,在AD上求作一点P,使得△ABC≌△APC,请保留清晰的作图痕迹.
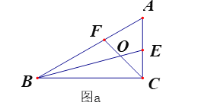
(2)如图a,在△ABC中, ∠ACB=![]() ,∠A=
,∠A=![]() ,BE、CF分别是∠ABC和∠ACB的角平分线,CF与BE相交于点O.请探究线段BC、BF、CE之间的关系,直接写出结论,不要求证明.
,BE、CF分别是∠ABC和∠ACB的角平分线,CF与BE相交于点O.请探究线段BC、BF、CE之间的关系,直接写出结论,不要求证明.
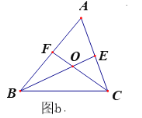
(3)如图b,若(2)中∠ACB为任意角,其它条件不变,请探究BC、BF、CE之间又有怎样的关系,请证明你的结论.
参考答案:
【答案】(1)答案见解析;(2)BC=BF+CE,证明见解析;(3)BC=BF+CE,证明见解析.
【解析】
(1)以点A为圆心,以AB长为半径画弧交AD于一点即可;
(2)在BC上截取BD=BF,首先证明△BFO≌△BDO,创造条件证明△COE≌△COD即可;
(3)在BC上截取BF'=BF,首先证明△BFO≌△BF'O,创造条件证明△COE≌△COF'即可.
(1)以点A为圆心,以AB长为半径画弧交AD于一点,则此点为所要求的点P.
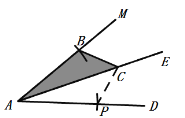
(2)线段BC、BF、CE之间的关系为:BC=BF+CE .
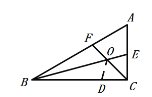
在BC上截取BD=BF.
在△BFO和△BDO中
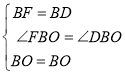
∴△BFO≌△BDO
∴∠BOF=∠BOD
∵∠A=![]() ,BE、CF分别是∠ABC和∠ACB的角平分线,CF与BE相交于点O.
,BE、CF分别是∠ABC和∠ACB的角平分线,CF与BE相交于点O.
∴∠BOC=180О-![]() ∠ABC-
∠ABC-![]() ∠ACB=180
∠ACB=180![]() -60
-60![]() =120
=120![]()
∴∠BOD=∠BOF=∠COE=180![]() -120
-120![]() =60
=60![]() .
.
∠COD=∠BOC-∠BOD=120![]() -60
-60![]() =60
=60![]()
在△COE和△COD中
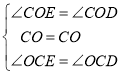
∴△COE≌△COD
∴CE=CD
∴BC=BF+CE .
(3)线段BC、BF、CE之间的关系为:BC=BF+CE .
在BC上截取BF'=BF.
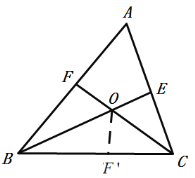
在△BFO和△BF'O中
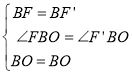
∴△BFO≌△BF'O
∴∠BOF=∠BOF'
∵∠A=60![]() ,BE、CF分别是∠ABC和∠ACB的角平分线,CF与BE相交于点O.
,BE、CF分别是∠ABC和∠ACB的角平分线,CF与BE相交于点O.
∴∠BOC=180О-![]() ∠ABC-
∠ABC-![]() ∠ACB=180
∠ACB=180![]() -60
-60![]() =120
=120![]()
∴∠BOF'=∠BOF=∠COE=180![]() -120
-120![]() =60
=60![]() .
.
∠COF'=∠BOC-∠BOF'=120![]() -60
-60![]() =60
=60![]()
在△COE和△COF'中
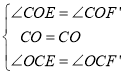
∴△COE≌△COF'
∴CE=CF'
∴BC=BF+CE .
-
科目: 来源: 题型:
查看答案和解析>>【题目】(模型建立)
(1)如图1,等腰直角三角形ABC中,∠ACB=90°,CB=CA,直线ED经过点C,过A作AD⊥ED于点D,过B作BE⊥ED于点E.
求证:△BEC≌△CDA;
(模型应用)
(2)① 已知直线l1:y=
 x+8与坐标轴交于点A、B,将直线l1绕点A逆时针旋转45
x+8与坐标轴交于点A、B,将直线l1绕点A逆时针旋转45 至直线l2,如图2,求直线l2的函数表达式;
至直线l2,如图2,求直线l2的函数表达式;② 如图3,长方形ABCO,O为坐标原点,点B的坐标为(8,-6),点A、C分别在坐标轴上,点P是线段BC上的动点,点D是直线y=-3x+6上的动点且在y轴的右侧.若△APD是以点D为直角顶点的等腰直角三角形,请直接写出点D的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】x2+(p+q)x+pq型式子是数学学习中常见的一类多项式,如何将这种类型的式子因式分解呢?因为(x+p)(x+q)= x2+(p+q)x+pq,所以,根据因式分解是与整式乘法方向相反的变形,利用这种关系可得:x2+(p+q)x+pq=(x+p)(x+q).如:x2+3x+2=x2+(1+2)x+1×2=(x+1)(x+2),上述过程还可以形象的用十字相乘的形式表示:先分解二次项系数,分别写在十字交叉线的左上角和左下角;再分解常数项,分别写在十字交叉线的右上角和右下角;然后交叉相乘,求代数和,使其等于一次项的系数,如下图.这样,我们可以得到:x2+3x+2= (x+1)(x+2),利用这种方法,将下列多项式分解因式:
(1)x2+7x+10
(2)-2x2-6x+36

-
科目: 来源: 题型:
查看答案和解析>>【题目】在日历上我们可以发现其中某些数满足一定的规律.如图是2018年8月份的日历,我们任意选择其中所示的方框部分,将方框部分中的4个位置的数交叉相乘,再相减,如8×16-9×15=-7,19×27-20×26=-7,不难发现结果都是-7.
(1)请你再选择一组数按上面的方式计算,看看是否符合这个规律.并用你擅长的表达方式描述这个规律.
(2)请你利用整式的运算对以上的规律加以证明.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在研究相似问题时,甲、乙同学的观点如下:
甲:将边长为3、4、5的三角形按图1的方式向外扩张,得到新三角形,它们的对应边间距为1,则新三角形与原三角形相似.
乙:将邻边为3和5的矩形按图2的方式向外扩张,得到新的矩形,它们的对应边间距均为1,则新矩形与原矩形不相似.
对于两人的观点,下列说法正确的是( )

A. 两人都对 B. 两人都不对 C. 甲对,乙不对 D. 甲不对,乙对
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图a,网格中的每一个正方形的边长为1,△ABC为格点三角形,直线MN为格点直线(点A、B、C、M、N在小正方形的顶点上).

(1)仅用直尺在图a中作出△ABC关于直线MN的对称图形△A′B′C′.
(2)如图b,仅用直尺将网格中的格点三角形ABC的面积三等分,并将其中的一份用铅笔涂成阴影.
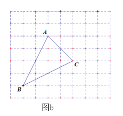
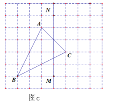
(3)如图c,仅用直尺作三角形ABC的边AC上的高,简单说明你的理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图a,P、Q是△ABC的边BC上的两点,且△APQ为等边三角形,AB=AC,
(1)求证:BP=CQ.
(2)如图a,若∠BAC=120
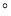 ,AP=3,求BC的长.
,AP=3,求BC的长.(3)若∠BAC=120
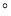 ,沿直线BC向右平行移动△APQ得到△A′P′Q′(如图b),A′Q′与AC交于点M.当点P移动到何处时,△AA′M≌△CQ′M?证明你的结论.
,沿直线BC向右平行移动△APQ得到△A′P′Q′(如图b),A′Q′与AC交于点M.当点P移动到何处时,△AA′M≌△CQ′M?证明你的结论.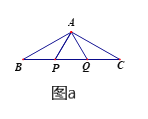

相关试题

