【题目】平行四边形ABCD中,BE⊥CD,BF⊥AD,垂足分别为E、F,若CE=2,DF=1,∠EBF=60°,求平行四边形ABCD的面积. 
参考答案:
【答案】解:∵BE⊥CD,BF⊥AD, ∴∠BEC=∠BFD=90°,
∵∠EBF=60°,
∵∠D+∠BED+∠BFD+∠EBF=360°,
∴∠D=120°,
∵平行四边形ABCD,
∴DC∥AB,AD∥BC,∠A=∠C
∴∠A=∠C=180°﹣120°=60°,
∴∠ABF=∠EBC=30°,
∴AD=BC=2EC=4
在△BEC中由勾股定理得:BE=2 ![]() ,
,
在△ABF中AF=4﹣1=3,
∵∠ABF=30,
∴AB=6,
∴平行四边形ABCD的面积是ABBE=6×2 ![]() =12
=12 ![]() .
.
答:平行四边形ABCD的面积是12 ![]()
【解析】根据四边形的内角和等于360°,求出∠D=120°,根据平行四边形的性质得到∠A=∠C=60°,进一步求出∠ABF=∠EBC=30°,根据CE=2,DF=1,求出BC、AB的长,根据勾股定理求出BE的长,根据平行四边形的面积公式即可求出答案.
【考点精析】利用三角形的内角和外角和含30度角的直角三角形对题目进行判断即可得到答案,需要熟知三角形的三个内角中,只可能有一个内角是直角或钝角;直角三角形的两个锐角互余;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角;在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:x3n﹣2÷xn+1=x3﹣nxn+2 , 求n的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知x4n+3÷xn+1=xn+3xn+5 , 求n的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,DE⊥AB,BF⊥CD,垂足分别为E,F.
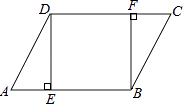
(1)求证:△ADE≌△CBF;
(2)求证:四边形BFDE为矩形. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在一次数学课外活动中,小明同学在点P处测得教学楼A位于北偏东60°方向,办公楼B位于南偏东45°方向.小明沿正东方向前进60米到达C处,此时测得教学楼A恰好位于正北方向,办公楼B正好位于正南方向.求教学楼A与办公楼B之间的距离(结果精确到0.1米).(供选用的数据:
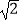 ≈1.414,
≈1.414, 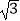 ≈1.732)
≈1.732)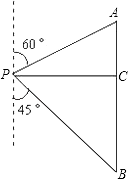
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列等式中成立的是( )
A.a4a=a4
B.a6﹣a3=a3
C.(ab2)3=a3b5
D.(a3)2=a6 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1是一副三角尺拼成的图案
(1)则∠EBC的度数为 _________ 度;
(2)将图1中的三角尺ABC绕点B旋转到AB⊥BD时,作∠DBC的角平分线BF,直接写出∠EBF的度数是 _________ 度;
(3)将图1中的三角尺ABC绕点B旋转α度(0°<α<90°)能否使∠ABE=2∠DBC?若能,则求出∠EBC的度数;若不能,说明理由.(图2、图3供参考)

相关试题

