【题目】商场销售某种冰箱,该种冰箱每台进价为2500元.已知原销售价为每台2900元时,平均每天能售出8台.若在原销售价的基础上每台降价50元,则平均每天可多售出4台.设每台冰箱的实际售价比原销售价降低了x元.
(1)填表(不需化简):
每天的销售量/台 | 每台销售利润/元 | |
降价前 | 8 | 400 |
降价后 |
(2)商场为使这种冰箱平均每天的销售利润达到5000元,则每台冰箱的实际售价应定为多少元?
参考答案:
【答案】(1)表格见解析;(2)每台冰箱的实际售价应定为2750元.
【解析】
试题分析:(1)设每台冰箱的实际售价比原销售价降低了![]() 元,根据在原销售价的基础上每台降价50元,则平均每天可多售出4台得出结果,填表即可;
元,根据在原销售价的基础上每台降价50元,则平均每天可多售出4台得出结果,填表即可;
(2)根据利润=售价-进价列出方程,求出方程的解即可得到结果.
试题解析:(1)填表如下:
每天的销售量/台 | 每台销售利润/元 | |
降价前 | 8 | 400 |
降价后 |
|
|
(2)根据题意,可得:![]() ,化简,整理得:
,化简,整理得:![]() 即
即![]() 解得:
解得:![]() ∴实际售价定为:2900-150=2750(元).答:每台冰箱的实际售价应定为2750元.
∴实际售价定为:2900-150=2750(元).答:每台冰箱的实际售价应定为2750元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】实数﹣27的立方根是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】“a是实数,|a|<0”这一事件是_____事件.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,
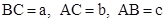 ,设c为最长边.当
,设c为最长边.当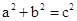 时,△ABC是直角三角形;当
时,△ABC是直角三角形;当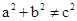 时,利用代数式
时,利用代数式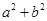 和
和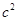 的大小关系,可以判断△ABC的形状(按角分类).
的大小关系,可以判断△ABC的形状(按角分类).(1)请你通过画图探究并判断:当△ABC三边长分别为6,8,9时,△ABC为____三角形;当△ABC三边长分别为6,8,11时,△ABC为______三角形.
(2)小明同学根据上述探究,有下面的猜想:“当
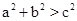 时,△ABC为锐角三角形;当
时,△ABC为锐角三角形;当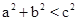 时,△ABC为钝角三角形.”请你根据小明的猜想完成下面的问题:
时,△ABC为钝角三角形.”请你根据小明的猜想完成下面的问题:当
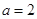 ,
,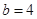 时,最长边c在什么范围内取值时,△ABC是直角三角形、锐角三角形、钝角三角形?
时,最长边c在什么范围内取值时,△ABC是直角三角形、锐角三角形、钝角三角形? -
科目: 来源: 题型:
查看答案和解析>>【题目】下列图形中,不是轴对称图形的是( )
A.角B.等边三角形C.平行四边形D.圆
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线y=﹣2(x﹣1)2+3,当x_____时,y随x的增大而减小.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在□ABCD中,E、F分别为边AB、CD的中点,连接DE、BF、BD.
(1)求证:△ADE≌△CBF;
(2)当AD⊥BD时,请你判断四边形BFDE的形状,并说明理由.

相关试题

