【题目】如图,在□ABCD中,E、F分别为边AB、CD的中点,连接DE、BF、BD.
(1)求证:△ADE≌△CBF;
(2)当AD⊥BD时,请你判断四边形BFDE的形状,并说明理由.

参考答案:
【答案】(1)证明见解析;(2)菱形,理由见解析
【解析】(1)根据平行四边形的性质即可证出△ADE与△CBF全等;(2)根据直角三角形斜边上的中线等于斜边的一半及平行四边形的判定即可证出四边形BFDE是菱形.
解:(1)证明:在平行四边形ABCD中,∠A=∠C,AD=BC,
∵E、F分别为AB、CD的中点,
∴AE=CF.
在△AED和△CFB中,

∴△AED≌△CFB(SAS);
(2)菱形,若AD⊥BD,则四边形BFDE是菱形.
证明:∵AD⊥BD,
∴△ABD是直角三角形,且∠ADB=90°.
∵E是AB的中点,
∴DE=![]() AB=BE.
AB=BE.
∵在ABCD中,E,F分别为边AB,CD的中点,
∴EB∥DF且EB=DF,
∴四边形BFDE是平行四边形.
∴四边形BFDE是菱形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】商场销售某种冰箱,该种冰箱每台进价为2500元.已知原销售价为每台2900元时,平均每天能售出8台.若在原销售价的基础上每台降价50元,则平均每天可多售出4台.设每台冰箱的实际售价比原销售价降低了x元.
(1)填表(不需化简):
每天的销售量/台
每台销售利润/元
降价前
8
400
降价后
(2)商场为使这种冰箱平均每天的销售利润达到5000元,则每台冰箱的实际售价应定为多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列图形中,不是轴对称图形的是( )
A.角B.等边三角形C.平行四边形D.圆
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线y=﹣2(x﹣1)2+3,当x_____时,y随x的增大而减小.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面材料:
点A、B在数轴上分别表示实数a、b,A、B两点之间的距离表示为∣AB∣.
当A、B两点中有一点在原点时,不妨设点A在原点,如图1,∣AB∣=∣OB∣=∣b∣=∣a-b∣;
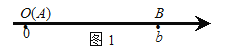
当A、B两点都不在原点时,如图2,点A、B都在原点的右边
∣AB∣=∣OB∣-∣OA∣=∣b∣-∣a∣=
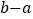 =∣a-b∣;
=∣a-b∣;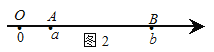
如图3,当点A、B都在原点的左边,
∣AB∣=∣OB∣-∣OA∣=∣b∣-∣a∣=
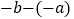 =∣a-b∣;
=∣a-b∣;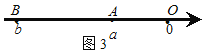
如图4,当点A、B在原点的两边,
∣AB∣=∣OB∣+∣OA∣=∣a∣+∣b∣=
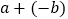 =∣a-b∣;
=∣a-b∣;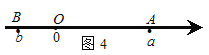
回答下列问题:
(1)数轴上表示1和6的两点之间的距离是 ,数轴上表示2和-3的两点之间的距离是 ;
(2)数轴上若点A表示的数是x,点B表示的数是-4,则点A和B之间的距离是 ,若∣AB∣=3,那么x为 ;
(3)当x是 时,代数式
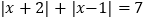 ;
; (4)若点A表示的数
 ,点B与点A的距离是10,且点B在点A的右侧,动点P、Q同时从A、B出发沿数轴正方向运动,点P的速度是每秒3个单位长度,点Q的速度是每秒
,点B与点A的距离是10,且点B在点A的右侧,动点P、Q同时从A、B出发沿数轴正方向运动,点P的速度是每秒3个单位长度,点Q的速度是每秒 个单位长度,求运动几秒后,点Q与点P 相距1个单位?(请写出必要的求解过程)
个单位长度,求运动几秒后,点Q与点P 相距1个单位?(请写出必要的求解过程) -
科目: 来源: 题型:
查看答案和解析>>【题目】因式分解:a2﹣3a= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,点M(﹣3,2)关于y轴对称的点的坐标为( )
A.(﹣3,﹣2)B.(﹣2,﹣3)C.(3,2)D.(3,﹣2)
相关试题

