【题目】如图,二次函数y=ax2+bx+2的图象与x轴交于点A(﹣1,0)、B(4,0),与y轴交于点C.
(1)a=;b=;
(2)点P为该函数在第一象限内的图象上的一点,过点P作PQ⊥BC于点Q,连接PC.
①求线段PQ的最大值;
②若以P、C、Q为顶点的三角形与△ABC相似,求点P的坐标.
参考答案:
【答案】
(1)﹣ ![]() ,
,![]()
(2)①由(1)知,a=﹣ ![]() ,b=
,b= ![]() ,
,
∴二次函数的解析式为y=﹣ ![]() x2+
x2+ ![]() x+2,
x+2,
如图,过点P作PG垂直于x轴于点G,与线段BC交于点M,

直线BC的表达式为y=﹣ ![]() x+2,则点M的坐标为(t,﹣
x+2,则点M的坐标为(t,﹣ ![]() t+2),
t+2),
则PM=yP﹣yM=(﹣ ![]() t2+
t2+ ![]() t+2)﹣(﹣
t+2)﹣(﹣ ![]() t+2)=﹣
t+2)=﹣ ![]() t2+2t
t2+2t
∵∠PQM=∠PGB,∠PMQ=GMB,
∴∠QPM=∠CBO
又∵∠PQM=∠COB,
∴△PQM∽△BOC,
∴ ![]()
∴PQ= ![]() PM=
PM= ![]() (﹣
(﹣ ![]() t2+2t)=﹣
t2+2t)=﹣ ![]() t(t﹣4)
t(t﹣4)
由抛物线的对称性可知,当t=2时,PQ的最大值是 ![]() =
= ![]()
②由①知,二次函数的解析式为y=﹣ ![]() x2+
x2+ ![]() x+2,
x+2,
∴C(0,2),
∴OC=2,
∵B(4,0),
∴OB=4,
设P(t,﹣ ![]() t2+
t2+ ![]() t+2),
t+2),
∴M(t,﹣ ![]() t+2)
t+2)
在Rt△OBC中,tan∠OBC= ![]() =
= ![]() ,
,
在Rt△BGM中,BG=4﹣t,
∴MG= ![]() (4﹣t),根据勾股定理得,
(4﹣t),根据勾股定理得,
BM= ![]() (4﹣t),
(4﹣t),
∵∠PQM=∠PGB,∠PMQ=GMB,
∴△PQM∽△BGM,
∴ ![]() ,=
,= ![]() ,
,
∴QM= ![]() PQ=
PQ= ![]() [﹣
[﹣ ![]() t(t﹣4)]=﹣
t(t﹣4)]=﹣ ![]() ,
,
∵B(4,0),C(0,2),
∴BC=2 ![]() ,
,
∴CQ=BC﹣QM﹣BM=2 ![]() +
+ ![]() ﹣
﹣ ![]() (4﹣t)=
(4﹣t)= ![]() =
= ![]() t(t+1)
t(t+1)
∵A(﹣1,0),B(4,0),C(0,2),
∴AB2=25,BC2=20,AC2=5,
∴AC2+BC2=AB2,
∴△ABC是直角三角形,
∴∠ACB=90°=∠PQC
∵以P、C、Q为顶点的三角形与△ABC相似,
∴①△PCQ∽△ABC,
∴ ![]() ,
,
∴ ![]() ,
,
∴t=3,
∴P(3,2)
②△CPQ∽△ABC,
∴ ![]() ,
,
∴ ![]() ,
,
∴t= ![]() ,
,
∴P( ![]() ,
, ![]() )
)
即:P的坐标为(3,2)或( ![]() ,
, ![]() ).
).
【解析】解:(1)∵二次函数y=ax2+bx+2的图象与x轴交于点A(﹣1,0)、B(4,0),
∴ ![]() ,
,
∴  ,
,
故答案为:﹣ ![]() ,
, ![]() ;
;
(1)利用待定系数法即可得出结论;
(2)先确定出PM,再判断出△PQM∽△BOC,得出PQ的长,即可得出结论;
(3)利用相似三角形的性质得出CQ,再分两种情况用相似三角形得出的比例式建立方程求解即可得出结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在矩形ABCD中,点P在AD上,AB=2,AP=1.将直角尺的顶点放在P处,直角尺的两边分别交AB,BC于点E,F,连接EF(如图①).

(1)当点E与点B重合时,点F恰好与点C重合(如图②),求PC的长;
(2)探究:将直尺从图②中的位置开始,绕点P顺时针旋转,当点E和点A重合时停止.在这个过程中,请你观察、猜想,并解答:
①tan∠PEF的值是否发生变化?请说明理由;
②直接写出从开始到停止,线段EF的中点经过的路线长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,三个村庄A,B,C之间的距离分别为
 ,已知A,B两村之间已修建了一条笔直的村级公路AB,为了实现村村通公路,现在要从C村修一条笔直公路CD直达AB,已知公路的造价为10000元/km,则修这条公路的最低造价是多少元?
,已知A,B两村之间已修建了一条笔直的村级公路AB,为了实现村村通公路,现在要从C村修一条笔直公路CD直达AB,已知公路的造价为10000元/km,则修这条公路的最低造价是多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在下图的直角坐标系中,将△ABC平移后得到△A’B’C’,它们的个顶点坐标如下表所示
△ABC
A(0,0)
B(3,0)
C(5,5)
△A'B'C'
A'(4,2)
B'(7,b)
C'(c,d)
(1)观察表中各对应点坐标的变化,并填空:△ABC向______平移______个单位长度,再向______平移______个单位长度可以得到△A'B'C';
(2)在坐标系中画出△ABC及平移后的△A'B'C';
(3)求出△A'B'C'的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】对某市中学生的幸福指数进行调查,从中抽取部分学生的调查表问卷进行统计,并绘制出不完整的统计表和条形统计图。
等级
频数
频率
★
60
★★
80
★★★
0.16
★★★★
0.30
★★★★★

(1)直接补全统计表;
(2)补全条形统计图(不要求写出计算过程);
(3)抽查的学生约占全市中学生的5%,估计全市约有多少名学生的幸福指数能达到五★级?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,以O为圆心的圆与直线y=﹣x+
 交于A、B两点,若△OAB恰为等边三角形,则弧AB的长度为( )
交于A、B两点,若△OAB恰为等边三角形,则弧AB的长度为( )
A. π
π
B.π
C. π
π
D. π
π -
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列材料:通过小学的学习我们知道,分数可分为“真分数”和“假分数”,而假分数都可化为常分数,如:
 =
=  =2+
=2+  =2
=2  .我们定义:在分式中,对于只含有一个字母的分式,当分子的次数大于或等于分母的次数时,我们称之为“假分式”;当分子的次数小于分母的次数时,我们称之为“真分式”.如
.我们定义:在分式中,对于只含有一个字母的分式,当分子的次数大于或等于分母的次数时,我们称之为“假分式”;当分子的次数小于分母的次数时,我们称之为“真分式”.如  ,
,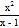 这样的分式就是假分式;再如:
这样的分式就是假分式;再如: ,
, 这样的分式就是真分式.类似的,假分式也可以化为带分式(即:整式与真分式的和的形式).如:
这样的分式就是真分式.类似的,假分式也可以化为带分式(即:整式与真分式的和的形式).如:
 =1-
=1- ;
; 解决下列问题:
(1)分式
 是 分式(填“真分式”或“假分式”);
是 分式(填“真分式”或“假分式”);(2)
 将假分式化为带分式;
将假分式化为带分式;(3)如果 x 为整数,分式
 的值为整数,求所有符合条件的 x 的值.
的值为整数,求所有符合条件的 x 的值.
相关试题

