【题目】已知:如图,在△ABC中,D是BC边上的一点,连接AD,取AD的中点E,过点A作BC的平行线与CE的延长线交于点F,连接DF.
(1)求证:AF=DC;
(2)请问:AD与CF满足什么条件时,四边形AFDC是矩形,并说明理由.

参考答案:
【答案】(1)见解析;(2)见解析.
【解析】
(1)因为AF∥DC,E为AD的中点,即可根据AAS证明△AEF≌△DEC,得出AF=DC即可;
(2)由(1)知,AF=DC且AF∥DC,可得四边形AFDC是平行四边形,又由AD=CF,故可根据对角线相等的平行四边形是矩形进行判定.
(1)∵AF∥DC,
∴∠AFE=∠DCE,
又∵E为AD的中点,
∴AE=DE,
在△AEF和△DEC中,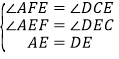 ,
,
∴△AEF≌△DEC(AAS),
∴AF=DC;
(2)当AD=CF时,四边形AFDC是矩形;理由如下:
由(1)得:AF=DC且AF∥DC,
∴四边形AFDC是平行四边形,
又∵AD=CF,
∴四边形AFDC是矩形(对角线相等的平行四边形是矩形).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平行四边形ABCD中,用直尺和圆规作∠BAD的平分线AG交BC于点E,若BF=6,AB=5,则AE的长为_____.

-
科目: 来源: 题型:
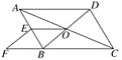
查看答案和解析>>【题目】如图,在ABCD中,对角线AC,BD交于点O,E为AB中点,点F在CB的延长线上,且EF∥BD.
(1)求证:四边形OBFE是平行四边形;
(2)当线段AD和BD之间满足什么条件时,四边形OBFE是矩形?并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】学校想知道九年级学生对我国倡导的“一带一路”的了解程度,随机抽取部分九年级学生进行问卷调查,问卷设有4个选项(每位被调查的学生必选且只选一项):A.非常了解.B.了解.C.知道一点.D.完全不知道.将调查的结果绘制如下两幅不完整的统计图,请根据两幅统计图中的信息,解答下列问题:
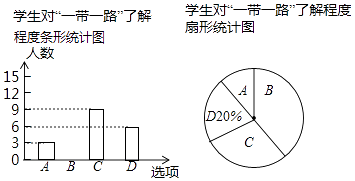
(1)求本次共调查了多少学生?
(2)补全条形统计图;
(3)该校九年级共有600名学生,请你估计“了解”的学生约有多少名?
(4)在“非常了解”的3人中,有2名女生,1名男生,老师想从这3人中任选两人做宣传员,请用列表或画树状图法求出被选中的两人恰好是一男生一女生的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,A,B,C三点坐标分别为A(﹣6,3),B(﹣4,1),C(﹣1,1).
(1)如图1,顺次连接AB,BC,CA,得△ABC.
①点A关于x轴的对称点A1的坐标是 , 点B关于y轴的对称点B1的坐标是;
②画出△ABC关于原点对称的△A2B2C2;
③tan∠A2C2B2=;
(2)利用四边形的不稳定性,将第二象限部分由小正方形组成的网格,变化为如图2所示的由小菱形组成的网格,每个小菱形的边长仍为1个单位长度,且较小内角为60°,原来的格点A,B,C分别对应新网格中的格点A′,B′,C′,顺次连接A′B′,B′C′,C′A′,得△A′B′C′,则tan∠A′C′B′= .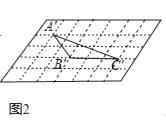
-
科目: 来源: 题型:
查看答案和解析>>【题目】我校50名学生在某一天调查了75户家庭丢弃塑料袋的情况,统计结果如下表:

根据上表回答下列问题:
(1)这天,一个家庭一天最多丢弃________个塑料袋.
(2)这天,丢弃3个塑料袋的家庭户数占总户数的________.
(3)该校所在的居民区共有居民0.8万户,则该区一天丢弃的塑料袋有多少个.
-
科目: 来源: 题型:
查看答案和解析>>【题目】点D,E分别是△ABC的边AB,AC的中点.
(1)如图1,点O是△ABC内的动点,点O,F分别是OB,OC的中点,求证:DEFG是平行四边形;
(2)如图2,若BE交DC于点O,请问AO的延长线经过BC的中点吗?为什么?

相关试题

