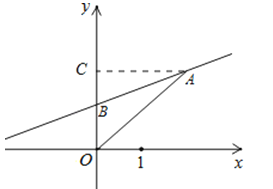
【题目】已知平面直角坐标系xOy(如图),直线 y=![]() x+b经过第一、二、三象限,与y轴交于点B,点A(2,t)在直线y=
x+b经过第一、二、三象限,与y轴交于点B,点A(2,t)在直线y=![]() x+b上,连结AO,△AOB的面积等于1.
x+b上,连结AO,△AOB的面积等于1.
(1)求b的值;
(2)如果反比例函数y=![]() (k是常量,k≠0)的图象经过点A,求这个反比例函数的表达式.
(k是常量,k≠0)的图象经过点A,求这个反比例函数的表达式.

参考答案:
【答案】(1)1(2)y=![]()
【解析】试题分析:(1)连接OA,过A作AC垂直于y轴,由A的横坐标为2得到AC=2,对于直线解析式,令y=0求出x的值,表示出OB的长,三角形AOB面积以OB为底,AC为高表示出来,根据已知三角形的面积求出OB的长,确定出B坐标,代入一次函数解析式中即可求出b的值;
(2)将A坐标代入一次函数求出t的值,确定出A坐标,将A坐标代入反比例解析式中求出k的值,即可确定出反比例解析式.
试题解析:解:(1)过A作AC⊥y轴,∵A(2,t),∴AC=2,对于直线y=![]() x+b,令x=0,得到y=b,即OB=b,∵S△AOB=
x+b,令x=0,得到y=b,即OB=b,∵S△AOB=![]() OBAC=OB=1,∴b=1;
OBAC=OB=1,∴b=1;
(2)由b=1,得到直线解析式为y=![]() x+1,将A(2,t)代入直线解析式得:t=1+1=2,即A(2,2),把A(2,2)代入反比例解析式得:k=4,则反比例解析式为y=
x+1,将A(2,t)代入直线解析式得:t=1+1=2,即A(2,2),把A(2,2)代入反比例解析式得:k=4,则反比例解析式为y=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一座桥如图,桥下水面宽度AB是20米,高CD是4米.要使高为3米的船通过,则其宽度须不超过多少米.
(1)如图1,若把桥看做是抛物线的一部分,建立如图坐标系.
①求抛物线的解析式;
②要使高为3米的船通过,则其宽度须不超过多少米?
(2)如图2,若把桥看做是圆的一部分.
①求圆的半径;
②要使高为3米的船通过,则其宽度须不超过多少米?

-
科目: 来源: 题型:
查看答案和解析>>【题目】直角三角形ABC中,∠C=90°,a,b,c分别为∠A,∠B,∠C的对边,若c﹣b=2,a=14,则b=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个样本数据按从小到大的顺序的排顺列为13、14、19、x、23、27、28、31,其中位数为22,则x等于( )
A. 21 B. 22 C. 20 D. 23
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系内,已知点A(2,2),B(-6,-4),C(2,-4).
(1)求△ABC的外接圆的圆心点M的坐标;
(2)求△ABC的外接圆在
 轴上所截弦DE的长;
轴上所截弦DE的长;
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商店购进一种商品,每件商品进价30元.试销中发现这种商品每天的销售量y(件)与每件销售价x(元)的关系数据如下:
x
30
32
34
36
y
40
36
32
28
(1)已知y与x满足一次函数关系,根据上表,求出y与x之间的关系式(不写出自变量x的取值范围);
(2)如果商店销售这种商品,每天要获得150元利润,那么每件商品的销售价应定为多少元?
(3)设该商店每天销售这种商品所获利润为w(元),求出w与x之间的关系式,并求出每件商品销售价定为多少元时利润最大?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,将一块腰长为
 的等腰直角三角板ABC放在第二象限,且斜靠在两坐标轴上,直角顶点C的坐标为(
的等腰直角三角板ABC放在第二象限,且斜靠在两坐标轴上,直角顶点C的坐标为(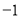 ,0),点B在抛物线
,0),点B在抛物线 上.
上.
(1)点A的坐标为 ,点B的坐标为 ;
(2)抛物线的解析式为 ;
(3)设(2)中抛物线的顶点为D,求△DBC的面积;
(4)在抛物线上是否还存在点P(点B除外),使ΔACP仍然是以AC为直角边的等腰直角三角形?若存在,请直接写出所有点P的坐标;若不存在,请说明理由。
相关试题

