【题目】如图,在等边△ABC中,点D,E分别在边BC,AB上,且BD=AE,AD与CE交于点F.
(1)求证:AD=CE;
(2)求∠DFC的度数.

参考答案:
【答案】(1)证明见解析(2)60°
【解析】试题分析:(1)根据△ABC是等边三角形,得到∠BAC=∠B=60°,AB=AC,再根据AE=BD可以利用SAS证得△AEC≌△BDA,从而证得AD=CE.
(2)根据△AEC≌△BDA得到∠ACE=∠BAD,然后求得∠DFC=∠FAC+∠ACE=∠FAC+∠BAD=60°,从而求得其正弦值.
试题解析:
证明:(1)在等边△ABC中,AB=BA,∠B=∠CAE
∴在△ACE和△BAD中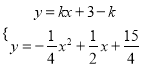
∴△ACE≌△BAD(SAS)
∴AD=CE
(2)∵△ACE≌△BAD(已证)
∴∠BAD=∠ACE,
而∠DFC=∠DAC+∠ACE
∴∠DFC=∠DAC+∠BAD=∠BAC=60°
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,AB、BC的垂直平分线相交于三角形内一点O,下列结论中,错误的是( )
A. 点O在AC的垂直平分线上
B. △AOB、△BOC、△COA都是等腰三角形
C. ∠OAB+∠OBC+∠OCA=90°
D. 点O到AB、BC、CA的距离相等
-
科目: 来源: 题型:
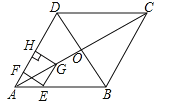
查看答案和解析>>【题目】如图,在菱形ABCD中,对角线AC与BD相交于点O,AB=8,∠BAD=60°,点E从点A出发,沿AB以每秒2个单位长度的速度向终点B运动,当点E不与点A重合时,过点E作EF⊥AD于点F,作EG∥AD交AC于点G,过点G作GH⊥AD交AD(或AD的延长线)于点H,得到矩形EFHG,设点E运动的时间为t秒
(1)求线段EF的长(用含t的代数式表示);
(2)求点H与点D重合时t的值;
(3)设矩形EFHG与菱形ABCD重叠部分图形的面积与S平方单位,求S与t之间的函数关系式;
(4)矩形EFHG的对角线EH与FG相交于点O′,当OO′∥AD时,t的值为 ;当OO′⊥AD时,t的值为 .
-
科目: 来源: 题型:
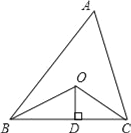
查看答案和解析>>【题目】如图,已知△ABC的周长是21,OB,OC分别平分∠ABC和∠ACB,OD⊥BC于D,且OD=3,△ABC的面积是__.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若式子3a﹣7与5﹣a的值互为相反数,则a的值为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知正数x的两个平方根是m+3和2m-15,则正数x= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知二次函数
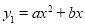 过(﹣2,4),(﹣4,4)两点.
过(﹣2,4),(﹣4,4)两点.(1)求二次函数
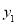 的解析式;
的解析式;(2)将
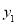 沿x轴翻折,再向右平移2个单位,得到抛物线
沿x轴翻折,再向右平移2个单位,得到抛物线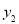 ,直线y=m(m>0)交
,直线y=m(m>0)交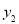 于M、N两点,求线段MN的长度(用含m的代数式表示);
于M、N两点,求线段MN的长度(用含m的代数式表示);(3)在(2)的条件下,
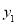 、
、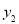 交于A、B两点,如果直线y=m与
交于A、B两点,如果直线y=m与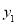 、
、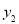 的图象形成的封闭曲线交于C、D两点(C在左侧),直线y=﹣m与
的图象形成的封闭曲线交于C、D两点(C在左侧),直线y=﹣m与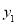 、
、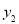 的图象形成的封闭曲线交于E、F两点(E在左侧),求证:四边形CEFD是平行四边形.
的图象形成的封闭曲线交于E、F两点(E在左侧),求证:四边形CEFD是平行四边形.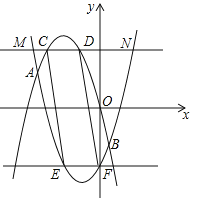
相关试题

