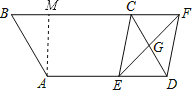
【题目】如图,平行四边形ABCD中,AB=3cm,BC=5cm,∠B=60°,G是CD的中点,E是边AD上的动点,EG的延长线与BC的延长线交于点F,连结CE,DF.

(1)求证:四边形CEDF是平行四边形;
(2)①当AE= cm时,四边形CEDF是矩形;②当AE= cm时,四边形CEDF是菱形.(直接写出答案,不需要说明理由)
参考答案:
【答案】(1)证明见解析;(2)3.5;2.
【解析】
试题分析:(1)证△CFG≌△EDG,推出FG=EG,根据平行四边形的判定推出即可;
(2)①求出△MBA≌△EDC,推出∠CED=∠AMB=90°,根据矩形的判定推出即可;
②求出△CDE是等边三角形,推出CE=DE,根据菱形的判定推出即可.
试题解析:(1)∵四边形ABCD是平行四边形,
∴CF∥ED,
∴∠FCG=∠EDG,
∵G是CD的中点,
∴CG=DG,
在△FCG和△EDG中,
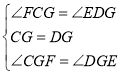 ,
,
∴△FCG≌△EDG(ASA)
∴FG=EG,
∵CG=DG,
∴四边形CEDF是平行四边形;
(2)①解:当AE=3.5时,平行四边形CEDF是矩形,
理由是:过A作AM⊥BC于M,
∵∠B=60°,AB=3,
∴BM=1.5,
∵四边形ABCD是平行四边形,
∴∠CDA=∠B=60°,DC=AB=3,BC=AD=5,
∵AE=3.5,
∴DE=1.5=BM,
在△MBA和△EDC中,
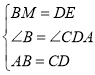 ,
,
∴△MBA≌△EDC(SAS),
∴∠CED=∠AMB=90°,
∵四边形CEDF是平行四边形,
∴四边形CEDF是矩形,
②当AE=2时,四边形CEDF是菱形,
理由是:∵AD=5,AE=2,
∴DE=3,
∵CD=3,∠CDE=60°,
∴△CDE是等边三角形,
∴CE=DE,
∵四边形CEDF是平行四边形,
∴四边形CEDF是菱形,
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知x+y=3,xy=﹣2.求(x﹣y)2的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】不等式2x-4≤0的解集是( )
A. x≥-2 B. x≤-2 C. x≥2 D. x≤2
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平面直角坐标系中,矩形OABC的对角线AC=12,∠ACO=30°
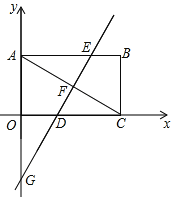
(1)求B、C两点的坐标;
(2)过点G(
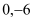 )作GF⊥AC,垂足为F,直线GF分别交AB、OC于点E、D,求直线DE的解析式;
)作GF⊥AC,垂足为F,直线GF分别交AB、OC于点E、D,求直线DE的解析式;(3)在⑵的条件下,若点M在直线DE上,平面内是否存在点P,使以O、F、M、P为顶点的四边形是菱形?若存在,请直接写出点P的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若a>b,要使ac<bc,则c________0.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市今年第一季度快递业务总量达到4210000件.4210000这个数用科学计数法表示为( )
A. 0.421×107 B. 4.21×106 C. 4.21×107 D. 4.21×104
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系内,已知直线
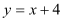 与x轴、y轴分别相交于点A和点C,抛物线
与x轴、y轴分别相交于点A和点C,抛物线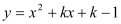 图像过点A和点C,抛物线与x轴的另一交点是B,
图像过点A和点C,抛物线与x轴的另一交点是B, 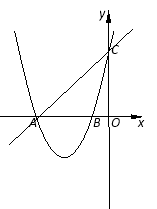
(1)求出此抛物线的解析式、对称轴以及B点坐标;
(2)若在y轴负半轴上存在点D,能使得以A、C、D为顶点的三角形与△ABC相似,请求出点D的坐标.
相关试题

