【题目】如图,在平面直角坐标系内,已知直线![]() 与x轴、y轴分别相交于点A和点C,抛物线
与x轴、y轴分别相交于点A和点C,抛物线![]() 图像过点A和点C,抛物线与x轴的另一交点是B,
图像过点A和点C,抛物线与x轴的另一交点是B,
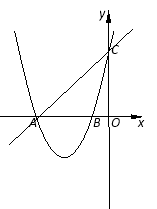
(1)求出此抛物线的解析式、对称轴以及B点坐标;
(2)若在y轴负半轴上存在点D,能使得以A、C、D为顶点的三角形与△ABC相似,请求出点D的坐标.
参考答案:
【答案】(1)![]() ,对称轴:直线
,对称轴:直线![]() ,B(-1,0)(2)D点坐标是(0,-
,B(-1,0)(2)D点坐标是(0,-![]() )
)
【解析】
试题分析:(1)求出点A和点C的坐标,然后代入![]() ,求出k的值可得函数解析式;然后可求出对称轴以及B点坐标;(2)分△CAD∽△ABC和△CDA∽△ABC两种情况讨论,利用相似三角形的性质可求出CD的长,然后可求出点D的坐标.
,求出k的值可得函数解析式;然后可求出对称轴以及B点坐标;(2)分△CAD∽△ABC和△CDA∽△ABC两种情况讨论,利用相似三角形的性质可求出CD的长,然后可求出点D的坐标.
试题解析:(1)∵直线![]() 与x轴、y轴分别相交于点A和点C
与x轴、y轴分别相交于点A和点C
∴得:A(-4,0), C(0,4)
∵抛物线![]() 图像过点A和点C,
图像过点A和点C,
代入点A或点C坐标得:k=5
∴![]()
对称轴:直线![]()
令y=0,得![]()
解方程得![]() ∴B(-1,0)
∴B(-1,0)
(2)AC=4![]() ,AB=3.
,AB=3.
根据题意, AO=CO=4,∴∠CAB=∠ACD= 45°
当△CAD∽△ABC时,CD︰AC=CA︰AB,
![]() 即CD︰4
即CD︰4![]() =4
=4![]() ︰3,∴CD=
︰3,∴CD=![]() ∴点
∴点![]() (0,-
(0,-![]() );
);
当△CDA∽△ABC时,CD︰AB=CA︰AC,
即CD=AB=3 , ∴点![]() (0,1);
(0,1);
∵点D在y轴负半轴上∴![]() (0,1)舍去
(0,1)舍去
∴综上所述:D点坐标是(0,-![]() )
)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平行四边形ABCD中,AB=3cm,BC=5cm,∠B=60°,G是CD的中点,E是边AD上的动点,EG的延长线与BC的延长线交于点F,连结CE,DF.

(1)求证:四边形CEDF是平行四边形;
(2)①当AE= cm时,四边形CEDF是矩形;②当AE= cm时,四边形CEDF是菱形.(直接写出答案,不需要说明理由)
-
科目: 来源: 题型:
查看答案和解析>>【题目】若a>b,要使ac<bc,则c________0.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市今年第一季度快递业务总量达到4210000件.4210000这个数用科学计数法表示为( )
A. 0.421×107 B. 4.21×106 C. 4.21×107 D. 4.21×104
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)
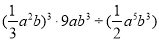
(2)(x2y+3)(x2y-3)
(3)(3mn+1)(3mn-1)-8m2n2
(4)(x+3y-2)(x-3y-2)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,⊙O是△ABC的外接圆,AB是⊙O的直径,FO⊥AB,垂足为点O,连接AF并延长交⊙O于点D,连接OD交BC于点E,∠B=30°,FO=
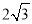 .
.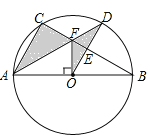
(1)求AC的长度;
(2)求图中阴影部分的面积.(计算结果保留根号)
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算(﹣3)﹣(﹣6)的结果等于( )
A.3
B.﹣3
C.9
D.18
相关试题

