练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

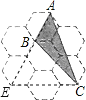
    【题目】如图是由7个形状、大小完全相同的正六边形组成的网格，正六边形的顶点称为格点．已知每个正六边形的边长为1，△ABC的顶点都在格点上，求△ABC的面积．

    【答案】2.

    【解析】试题分析: 延长AB，然后作出过点C与格点所在的直线，一定交于格点E，根据S△ABC=S△AEC-S△BEC即可求解．

    试题解析:

    延长AB，再作出过点C与格点所在的直线，交于格点E.

    ∵正六边形的边长为1，

    ∴正六边形的半径是1，则CE＝4，

    由题意得中间间隔一个顶点的两个顶点之间的距离是，

    则△BCE的边EC上的高是，△ACE边EC上的高是，

    则S△ABC＝S△AEC－S△BEC＝×4×(－)＝2.

    点睛: 本题考查了正多边形的计算，正确理解S△ABC＝S△AECS△BEC是关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】近似数9.80万有______个有效数字.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，△ABC与△CDE都是等边三角形，点E、F分别为AC、BC的中点．

    （1）求证：四边形EFCD是菱形；

    （2）如果AB=8，求D、F两点间的距离．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】定义运算：ab=a(1﹣b)．若a，b是方程x2﹣x+m=0(m＜0)的两根，则bb﹣aa的值为（ ）

    A. 0 B. 1 C. 2 D. 与m有关

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】关于x的方程（k﹣1）x2+2kx+2=0．

    （1）求证：无论k为何值，方程总有实数根．

    （2）设x1，x2是方程（k﹣1）x2+2kx+2=0的两个根，记，S的值能为2吗？若能，求出此时k的值；若不能，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下列语句：①顶角、底角都相等的两个等腰三角形一定全等；②两个等边三角形一定是全等图形；③如果两个三角形全等，它们的形状和大小一定都相同； ④三个角一一对应相等的两个三角形一定全等．其中错误的说法有（　　）

    A. 4个B. 3个C. 2个D. 1个

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下列计算正确的是 （ ）

    A. 7a-a=6 B. a2·a3=a5 C. (a3)3=a6 D. (ab)4=ab4

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】压路机的滚轮转动一周能压多少路面是指( )。

    A.滚轮的两个圆面积B.滚轮的表面积C.滚轮的侧面积D.滚轮的体积

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】利用图形面积之间的关系求不确定事件的概率，称为__________，某事件发生的概率P(A)＝事件发生所有可能结果组成的图形面积÷所有可能结果组成的图形的面积．

    查看答案和解析>>

    同步练习册答案