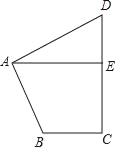
【题目】如图,在四边形ABCD中,∠BAD=∠C=90°,AB=AD,AE⊥CD,垂足为E,若线段AE=10,则S四边形ABCD=_____.
参考答案:
【答案】100
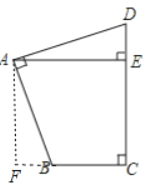
【解析】试题分析:过A作AF⊥BC,交CB的延长线于F,
∵AE⊥CD,∠C=90°
∴∠AED=∠F=∠C=90°,∴四边形AFCE是矩形,
∴∠FAE=90°,
∵∠DAB=90°,
∴∠DAE=∠BAF=90°﹣∠BAE,
在△AFB和△AED中,
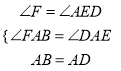 ,
,
∴△AFB≌△AED(AAS),
∴AE=AF=10,S△AFB=S△AED,
∵四边形AFCE是矩形,
∴四边形AFCE是正方形,
∴S正方形AFCE=10×10=100,
∴S四边形ABCD
=S四边形ABCE+S△AED
=S四边形ABCE+S△AFB
=S正方形AFCE
=100.
-
科目: 来源: 题型:
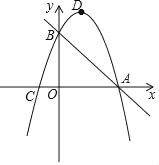
查看答案和解析>>【题目】已知,如图,抛物线y=﹣x2+bx+c经过直线y=﹣x+3与坐标轴的两个交点A,B,此抛物线与x轴的另一个交点为C,抛物线的顶点为D.
(1)求此抛物线的解析式;
(2)若点M为抛物线上一动点,是否存在点M,使△ACM与△ABC的面积相等?若存在,求点M的坐标;若不存在,请说明理由.
(3)在x轴上是否存在点N使△ADN为直角三角形?若存在,确定点N的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,要建一个面积为140平方米的仓库,仓库的一边靠墙,这堵墙长16米;在与墙平行的一边,要开一扇2米宽的门.已知围建仓库的现有木板材料可使新建板墙的总长为32米,那么这个仓库设计的长和宽应分别为多少米?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,A点的坐标为(1,0).以OA为边在x轴上方画一个正方形OABC.以原点O为圆心,正方形的对角线OB长为半径画弧,与x轴正半轴交于点D.
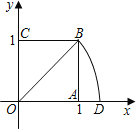
(1)点D的坐标是 ;
(2)点P(x,y),其中x,y满足2x-y=-4.
①若点P在第三象限,且△OPD的面积为3
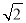 ,求点P的坐标;
,求点P的坐标;②若点P在第二象限,判断点E(
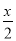 +1,0)是否在线段OD上,并说明理由.
+1,0)是否在线段OD上,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】解下列方程
(1)2x2﹣4x=12
(2)4x(2x+1)=6x+3.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,∠1=65°,则∠A+∠B+∠C+∠D+∠E+∠F的度数为___________.
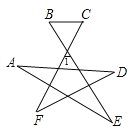
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图,点A,B,C,D在一条直线上,填写下列空格:
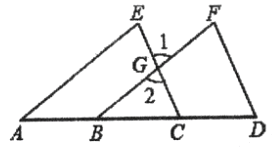
∵AE∥BF(已知)
∴∠E=∠1(______________________)
∵∠E=∠F(已知〉
∴∠_____=∠F(________________)
∴________∥_________(________________________)
相关试题

