【题目】已知O是直线上的一点,∠AOB是直角,OE平分∠AOC
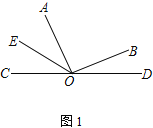
(1) 在图①中,若∠BOD=28°,求∠AOE的度数
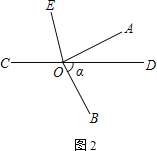
(2) 将图①中的∠AOB绕顶点O顺时针旋转至图②的位置.若∠BOD=α,试用含α的式子表示∠AOE,并说明理由
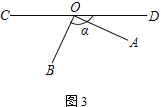
(3) 继续旋转AOB至图③的位置,若∠BOD=α,其他条件不变,试将图形补充完整,求∠AOE的度数.(用含α的式子表示)
参考答案:
【答案】(1)∠AOE=31°;(2)∠AOE=45°+![]() α,理由见解析;(3)作图见解析,∠AOE=135°-
α,理由见解析;(3)作图见解析,∠AOE=135°-![]() α.
α.
【解析】
(1)求出∠AOC,根据角平分线定义求出∠AOE,即可求出答案;
(2)求出∠AOD和∠AOC,根据角平分线定义即可求出答案;
(3)求出∠AOD和∠AOC,根据角平分线定义即可求出答案;
解:(1)∵∠AOB是直角,∠BOD=28°,
∴∠AOC=180°-∠AOB-∠BOD=180°-90°-28°=62°,
∵OE平分∠AOC,
∴∠AOE=![]() ∠AOC=
∠AOC=![]() ×62°=31°;
×62°=31°;
(2)∠AOE=45°+![]() α,理由如下:
α,理由如下:
∵∠AOB是直角,∠BOD=α,
∴∠AOD=90°-α,
∵∠AOD+∠AOC=180°,
∴∠AOC=180°-∠AOD=180°-(90°-α)= 90°+α,
∵OE平分∠AOC,
∴∠AOE=![]() ∠AOC=
∠AOC=![]() ×(90°+α)=45°+
×(90°+α)=45°+![]() α;
α;
(3)如图,
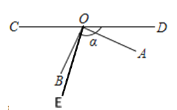
∵∠AOB是直角,∠BOD=α,
∴∠AOD=α-90°,
∵∠AOD+∠AOC=180°,
∴∠AOC=180°-∠AOD=180°-(α-90°)= 270°-α,
∵OE平分∠AOC,
∴∠AOE=![]() ∠AOC=
∠AOC=![]() ×(270°-α)=135°-
×(270°-α)=135°-![]() α.
α.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校初中三年级270名师生计划集体外出一日游,乘车往返,经与客运公司联系,他们有座位数不同的中巴车和大客车两种车型可供选择,每辆大客车比中巴车多15个座位,学校根据中巴车和大客车的座位数计算后得知,如果租用中巴车若干辆,师生刚好坐满全部座位;如果租用大客车,不仅少用一辆,而且师生坐完后还多30个座位.
(1)求中巴车和大客车各有多少个座位?
(2)客运公司为学校这次活动提供的报价是:租用中巴车每辆往返费用350元,租用大客车每辆往返费用400元,学校在研究租车方案时发现,同时租用两种车,其中大客车比中巴车多租一辆,所需租车费比单独租用一种车型都要便宜,按这种方案需要中巴车和大客车各多少辆?租车费比单独租用中巴车或大客车各少多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,直线
 :
: 分别与x轴、y轴交于点B、C,且与直线
分别与x轴、y轴交于点B、C,且与直线 :
: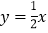 交于点A.
交于点A. 分别求出点A、B、C的坐标;
分别求出点A、B、C的坐标; 直接写出关于x的不等式
直接写出关于x的不等式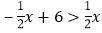 的解集;
的解集; 若D是线段OA上的点,且
若D是线段OA上的点,且 的面积为12,求直线CD的函数表达式.
的面积为12,求直线CD的函数表达式.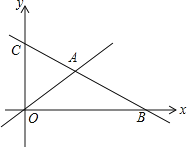
-
科目: 来源: 题型:
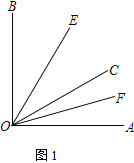
查看答案和解析>>【题目】已知∠AOB内部有3条射线OE、OC、OF
(1) 如图1,若∠AOB = 90°,∠AOC = 30°,OE平分∠BOC,OF平分∠AOC,求∠EOF的度数.
(2) 如图2,若∠AOB = α,∠EOB = ∠COB,∠COF = ∠FOA,求∠EOF的度数(用含α的式子表示)
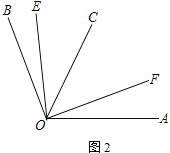
-
科目: 来源: 题型:
查看答案和解析>>【题目】在数轴上和有理数 a、b、c 对应的点的位置如图所示,有下面四个结论:①abc<0;②|a﹣b|+|b﹣c|=|a﹣c|③(a﹣b)(b﹣c)(c﹣a)>0;④|a|<1﹣bc,其中正确的结论有______.

-
科目: 来源: 题型:
查看答案和解析>>【题目】商店只有雪碧、可乐、果汁、奶汁四种饮料,每种饮料数量充足,某同学去该店购买饮料,每种饮料被选中的可能性相同.
(1)若他去买一瓶饮料,则他买到奶汁的概率是;
(2)若他两次去买饮料,每次买一瓶,且两次所买饮料品种不同,请用树状图或列表法求出他恰好买到雪碧和奶汁的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】某商店购买一批单价为20元的日用品,如果以单价30元销售,那么半月内可以售出400件.据销售经验,提高销售单价会导致销售量的减少,即销售单价每提高一元,销售量相应减少20件.如何提高销售价,才能在半月内获得最大利润?
相关试题

