Question

【题目】如图，在平面直角坐标系中，坐标原点O是菱形ABCD的对称中心．边AB与x轴平行，点B（1，-2），反比例函数（k≠0）的图象经过A，C两点．

（1）求点C的坐标及反比例函数的解析式．

（2）直线BC与反比例函数图象的另一交点为E，求以O，C，E为顶点的三角形的面积．

Answer 1

【答案】（1）C（4，2），；（2）．

【解析】试题分析：（1）连结AC，BD，根据坐标原点O是菱形ABCD的对称中心，可得AC，BD相交于点O，且∠AOB=90°，根据B（1，﹣2），且AB∥x轴，可设A（a，﹣2），则AO2=a2+4，BO2=5，AB2=（1﹣a）2，在Rt△AOB中，由勾股定理可得A（﹣4，﹣2），C（4，2），再根据待定系数法可求反比例函数解析式；

（2）连结OE，则△OCE是以O，C，E为顶点的三角形，根据待定系数法可求直线BC的解析式，求出其与y轴交于点F的坐标，解方程可求点E的横坐标，再根据三角形面积公式即可求解．

试题解析：解：（1）连结AC，BD，∵坐标原点O是菱形ABCD的对称中心，∴AC，BD相交于点O，且∠AOB=90°，∵B（1，﹣2），且AB∥x轴，∴设A（a，﹣2），则AO2=a2+4，BO2=5，AB2=（1﹣a）2，在Rt△AOB中，由勾股定理得（1﹣a）2=a2+4+5，解得a=﹣4，∴A（﹣4，﹣2），∴C（4，2），∵反比例函数（k≠0）的图象经过A，C两点，∴反比例函数解析式为；

（2）连结OE，则△OCE是以O，C，E为顶点的三角形，设直线BC的解析式为y=kx+b，∵点B（1，﹣2），C（4，2）在该直线上，∴，解得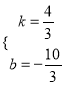： ，∴直线BC的解析式为，设其与y轴交于点F（0， ），∵反比例函数为，∴，解得x1=4，x2=，∴点E的横坐标为，∴以O，C，E为顶点的三角形的面积==．