【题目】如图,锐角三角形ABC中,直线L为BC的中垂线.直线M为∠ABC的角平分线,L与M相交于P点.若∠A=60![]() ,∠ACP=24
,∠ACP=24![]() ,则∠ABP的度数( )
,则∠ABP的度数( )
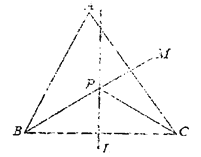
A. 24![]() B. 30
B. 30![]() C. 32
C. 32![]() D. 36
D. 36![]()
参考答案:
【答案】C
【解析】![]() 直线m为∠ABC的角平分线,
直线m为∠ABC的角平分线,
∴∠ABP=∠CBP.
∵直线l为BC的中垂线,
∴PB=PC,
∴∠CBP=∠BCP
∴∠ABP=∠CBP=∠BCP.
在锐角△ABC中,
3∠ABP+∠A+∠ACP=180°,
又∵∠A=60°,∠ACP=24°,
3∠ABP+60°+24°=180°,
∴∠ABP=32°.
本题考查的是线段垂直平分线的性质、角平分线的性质,掌握线段的垂直平分线上的点到线段的两个端点的距离相等是解题的关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(本题满分10分)科幻小说《实验室的故事》中,有这样一个情节,科学家把一种珍奇的植物分别放在不同温度的环境中,经过一天后,测试出这种植物高度的增长情况(如下表):
温度
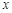 /℃
/℃……
-4
-2
0
2
4
4.5
……
植物每天高度增长量
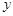 /mm
/mm……
41
49
49
41
25
19.75
……
由这些数据,科学家推测出植物每天高度增长量
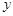 是温度
是温度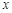 的函数,且这种函数是反比例函数、一次函数和二次函数中的一种.
的函数,且这种函数是反比例函数、一次函数和二次函数中的一种.(1)请你选择一种适当的函数,求出它的函数关系式,并简要说明不选择另外两种函数的理由;
(2)温度为多少时,这种植物每天高度的增长量最大?
(3)如果实验室温度保持不变,在10天内要使该植物高度增长量的总和超过250mm,那么实验室的温度
 应该在哪个范围内选择?请直接写出结果.
应该在哪个范围内选择?请直接写出结果. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,过点B(6,0)的直线AB与直线OA相交于点A(4,2),动点M沿路线O→A→C运动.
(1)求直线AB的解析式.
(2)求△OAC的面积.
(3)当△OMC的面积是△OAC的面积的
 时,求出这时点M的坐标.
时,求出这时点M的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在同一平面直角坐标系中,函数y=ax2+bx与y=bx+a的图像可能是( )
A.
 B.
B.  C.
C. 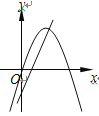 D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,是二次函数 y=ax2+bx+c(a≠0)的图象的一部分, 给出下列命题 :①a+b+c=0;②b>2a;③ax2+bx+c=0的两根分别为-3和1;④a-2b+c>0.其中正确的命题是__________.(只要求填写正确命题的序号)

-
科目: 来源: 题型:
查看答案和解析>>【题目】某商店经销一种成本为每千克40元的水产品,据市场分析,若按每千克50元销售,一个月能售出500千克.若销售价每涨1元,则月销售量减少10千克.
(1)要使月销售利润达到最大,销售单价应定为多少元?
(2)要使月销售利润不低于8000元,请结合图象说明销售单价应如何定?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图,△ABC是等边三角形,AE=CD,BQ⊥AD于Q,BE交AD于点P,下列说法:①∠APE=∠C,② AQ=BQ,③BP=2PQ, ④AE+BD=AB,其正确的个数有( )个.

A. 1 B. 2 C. 3 D. 4
相关试题

