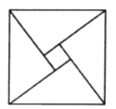
【题目】2002年8月在北京召开的国际数学家大会会标取材于我国古代数学家赵爽的《勾股圆方图》,它是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形(如图).如果大正方形的面积是100,小正方形的面积是4,直角三角形较短的直角边长为![]() ,较长的直角边长为
,较长的直角边长为![]() ,那么
,那么![]() 的值是_________.
的值是_________.
参考答案:
【答案】196
【解析】
根据大正方形的面积即可求得c2,利用勾股定理可以得到a2+b2=c2,然后求得直角三角形的面积即可求得ab的值,根据(a+b)2=a2+b2+2ab=c2+2ab即可求解.
如图,
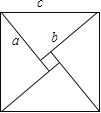
∵大正方形的面积是100,
∴c2=100,
∴a2+b2=c2=100,
∵直角三角形的面积是(1004)÷4=24,
又∵直角三角形的面积是![]()
∴ab=48,
∴![]()
故答案为:![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC是⊙O的内接三角形,BC=
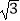 .如图,若AC是⊙O的直径,∠BAC=60°,延长BA到点D,使得DA=
.如图,若AC是⊙O的直径,∠BAC=60°,延长BA到点D,使得DA=  BA,过点D作直线l⊥BD,垂足为点D,请将图形补充完整,判断直线l和⊙O的位置关系并说明理由.
BA,过点D作直线l⊥BD,垂足为点D,请将图形补充完整,判断直线l和⊙O的位置关系并说明理由. 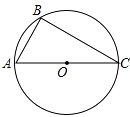
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
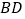 是
是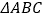 的外角
的外角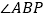 的平分线,
的平分线,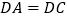 ,
,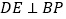 于点
于点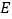 .若
.若 ,则
,则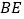 的长是( )
的长是( )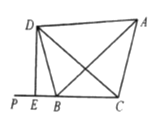
A. 2 B. 1.5 C. 1 D. 0.5
-
科目: 来源: 题型:
查看答案和解析>>【题目】大学毕业生小王相应国家“自主创业”的号召,利用银行小额无息贷款开办了一家饰品店.该店购进一种今年新上市的饰品进行销售,饰品的进价为每件40元,售价为每件60元,每月可卖出300件.市场调查反映:调整价格时,售价每涨1元每月要少卖10件;售价每下降1元每月要多卖20件.为了获得更大的利润,现将饰品售价调整为60+x(元/件)(x>0即售价上涨,x<0即售价下降,其中x为整数),每月饰品销量为y(件),月利润为w(元).
(1)直接写出y与x之间的函数关系式;
(2)如何确定销售价格才能使月利润最大?求最大月利润? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,A,B为x轴上两点,C、D为y轴上的两点,经过点A,C,B的抛物线的一部分C2组合成一条封闭曲线,我们把这条封闭曲线成为“蛋线”.已知点C的坐标为(0,﹣
 ),点M是抛物线C2:y=mx2﹣2mx﹣3m(m<0)的顶点.
),点M是抛物线C2:y=mx2﹣2mx﹣3m(m<0)的顶点.
(1)求A、B两点的坐标;
(2)“蛋线”在第四象限上是否存在一点P,使得△PBC的面积最大?若存在,求出△PBC面积的最大值;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知在△ABC中,点D , E , F分别是边AB , AC , BC上的点,DE∥BC , EF∥AB , 且AD:DB=4:7,那么CF:CB等于( )

A.7:11
B.4:8
C.4:7
D.3:7 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在长方形
 的对称轴
的对称轴 上找点
上找点 ,使得
,使得 ,
, 均为等腰三角形,则满足条件的点
均为等腰三角形,则满足条件的点 有_________个.
有_________个.
相关试题

