【题目】如图1,点O为直线AB上一点,过点O作射线OC,使∠BOC=120°.将一直角三角板的直角顶点放在点O处,一边OM在射线OB上,另一边ON在直线AB的下方. 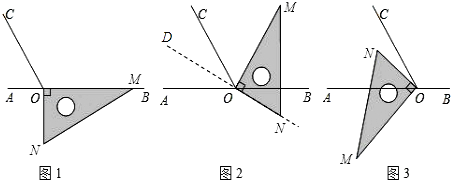
(1)将图1中的三角板绕点O逆时针旋转至图2,使一边OM在∠BOC的内部,且恰好平分∠BOC.问:此时直线ON是否平分∠AOC?请说明理由.
(2)将图1中的三角板绕点O顺时针旋转至图3,使ON在∠AOC的内部,求∠AOM﹣∠NOC的度数.
参考答案:
【答案】
(1)解:直线ON平分∠AOC.
理由如下:
如图,设ON的反向延长线为OD,
∵OM平分∠BOC,
∴∠MOC=∠MOB= ![]() ,
,
又∠MOD=∠MON=90°,
∴∠COD=90°﹣∠BOC=30°,
∵∠AOC=180°﹣∠BOC=60°,
∴∠COD= ![]() ∠AOC,
∠AOC,
∴OD平分∠AOC,
即直线ON平分∠AOC
(2)解:∵∠MON=90°,∠AOC=60°,
∴∠AOM=90°﹣∠AON,∠NOC=60°﹣∠AON,
∴∠AOM﹣∠NOC=(90°﹣∠AON)﹣(60°﹣∠AON)=30°.
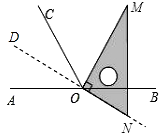
【解析】(1)设ON的反向延长线为OD,由旋转的性质可知∠M=30°,∠MNO=60°,从而可分别求得∠BON=∠AOD=∠COD=30°;(2)分别用∠AON表示出∠AOM和∠NOC即可.
【考点精析】通过灵活运用旋转的性质,掌握①旋转后对应的线段长短不变,旋转角度大小不变;②旋转后对应的点到旋转到旋转中心的距离不变;③旋转后物体或图形不变,只是位置变了即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若xp+4x3-qx2-2x+5是关于x五次四项式,则-p+q= 。
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的是( )
A.两个矩形一定相似
B.两个菱形一定相似
C.两个等腰三角形一定相似
D.两个等边三角形一定相似 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知2m×2m×4=28,则m=________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】不解方程3x2+5x﹣4=0,可以判断它的根的情况是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】一元二次方程x2﹣16=0的根是( )
A.x=2
B.x=4
C.x1=2,x2=﹣2
D.x1=4,x2=﹣4 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB为⊙O的直径,点C在⊙O上,过点C作⊙O的切线交AB的延长线于点D,已知∠D=30°.
(1)求∠A的度数;
(2)若点F在⊙O上,CF⊥AB,垂足为E,CF=
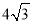 ,求图中阴影部分的面积.
,求图中阴影部分的面积. 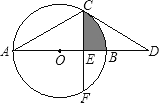
相关试题

