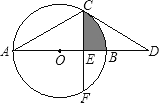
【题目】如图,AB为⊙O的直径,点C在⊙O上,过点C作⊙O的切线交AB的延长线于点D,已知∠D=30°.
(1)求∠A的度数;
(2)若点F在⊙O上,CF⊥AB,垂足为E,CF=![]() ,求图中阴影部分的面积.
,求图中阴影部分的面积.
参考答案:
【答案】(1) 30°;(2)![]() -2
-2![]() .
.
【解析】试题分析:(1)连接OC,则△OCD是直角三角形,可求出∠COD的度数;由于∠A与∠COD是同弧所对的圆周角与圆心角.根据圆周角定理即可求得∠A的度数;
(2)由图可知:阴影部分的面积是扇形OCB和Rt△OEC的面积差;那么解决问题的关键是求出半径和OE的长;在Rt△OCE中,∠OCE=∠D=30°,已知了CE的长,通过解直角三角形,即可求出OC、OE的长,由此得解.
试题解析:(1)连接OC,
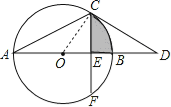
∵CD切⊙O于点C
∴∠OCD=90°
∵∠D=30°
∴∠COD=60°
∵OA=OC
∴∠A=∠ACO=30°;
(2)∵CF⊥直径AB,CF=4![]()
∴CE=2![]()
∴在Rt△OCE中,tan∠COE=![]() ,
,
OE=![]() =2,
=2,
∴OC=2OE=4
∴S扇形BOC=![]() ,S△EOC=
,S△EOC=![]() ×2×2
×2×2![]() =2
=2![]()
∴S阴影=S扇形BOC-S△EOC=![]() -2
-2![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,点O为直线AB上一点,过点O作射线OC,使∠BOC=120°.将一直角三角板的直角顶点放在点O处,一边OM在射线OB上,另一边ON在直线AB的下方.
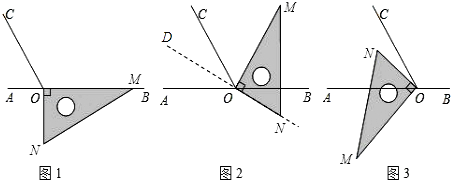
(1)将图1中的三角板绕点O逆时针旋转至图2,使一边OM在∠BOC的内部,且恰好平分∠BOC.问:此时直线ON是否平分∠AOC?请说明理由.
(2)将图1中的三角板绕点O顺时针旋转至图3,使ON在∠AOC的内部,求∠AOM﹣∠NOC的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】不解方程3x2+5x﹣4=0,可以判断它的根的情况是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】一元二次方程x2﹣16=0的根是( )
A.x=2
B.x=4
C.x1=2,x2=﹣2
D.x1=4,x2=﹣4 -
科目: 来源: 题型:
查看答案和解析>>【题目】在一款名为超级玛丽的游戏中,玛丽到达一个高为10米的高台A,利用旗杆顶部的绳索,划过90°到达与高台A水平距离为17米,高为3米的矮台B,

(1)求高台A比矮台B高多少米?
(2)求旗杆的高度OM;
(3)玛丽在荡绳索过程中离地面的最低点的高度MN.
-
科目: 来源: 题型:
查看答案和解析>>【题目】推理填空
依据下列解方程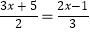 的过程,请在前面的括号内填写变形步骤,在后面的括号内填写变形依据.
的过程,请在前面的括号内填写变形步骤,在后面的括号内填写变形依据.
解:去分母,得3(3x+5)=2(2x﹣1).()
去括号,得9x+15=4x﹣2()
(),得9x﹣4x=﹣15﹣2.()
合并,得5x=﹣17()
(),得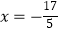 .()
.() -
科目: 来源: 题型:
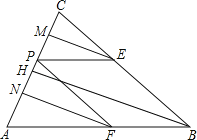
查看答案和解析>>【题目】如图,△ABC中,AB=BC,AC=8,tanA=k,P为AC边上一动点,设PC=x,作PE∥AB交BC于E,PF∥BC交AB于F.
(1)证明:△PCE是等腰三角形;
(2)EM、FN、BH分别是△PEC、△AFP、△ABC的高,用含x和k的代数式表示EM、FN,并探究EM、FN、BH之间的数量关系;
(3)当k=4时,求四边形PEBF的面积S与x的函数关系式.x为何值时,S有最大值?并求出S的最大值.
相关试题

