【题目】作图与计算:
在如图所示的正方形网格中,每个小正方形的边长为![]() ,格点三角形(顶点是网格线的交点的三角形)
,格点三角形(顶点是网格线的交点的三角形)![]() 的顶点
的顶点![]() ,
,![]() 的坐标分别为
的坐标分别为![]() ,
,![]() .
.

(1)请在如图所示的网格平面内作出平面直角坐标系;
(2)请作出![]() 关于
关于![]() 轴对称的
轴对称的![]() ;
;
(3)直接写出![]() 的面积及点
的面积及点![]() 的坐标.
的坐标.
参考答案:
【答案】(1)坐标系见解析;(2)见解析;(3)![]() ,
,![]() .
.
【解析】
(1)根据A点坐标建立平面直角坐标系即可;
(2)作出各点关于y轴的对称点,再顺次连接即可;
(3)利用矩形的面积减去三个顶点上三角形的面积即可;根据点B1在坐标系中的位置写出其坐标即可.
(1)根据题意可作出如图所示的坐标系;
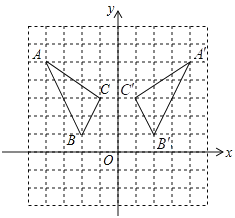
(2)如图,![]() 即为所求;
即为所求;
(3)S△ABC=3×4-![]() ×2×4-
×2×4-![]() ×2×1-
×2×1-![]() ×2×3=12-4-1-3=4,由图可知,
×2×3=12-4-1-3=4,由图可知,![]() (2,1)..
(2,1)..
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC中,∠ABC=45°,AB=7
 ,BC=17,以AC为斜边在△ABC外作等腰Rt△ACD,连接BD,则BD的长为___.
,BC=17,以AC为斜边在△ABC外作等腰Rt△ACD,连接BD,则BD的长为___.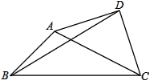
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,甲、乙两渔船同时从港口O出发外出捕鱼,乙沿南偏东
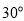 方向以每小时15海里的速度航行,甲沿南偏西
方向以每小时15海里的速度航行,甲沿南偏西 方向以每小时
方向以每小时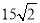 海里的速度航行,当航行1小时后,甲在A处发现自己的渔具掉在乙船上,于是迅速改变航向和速度,仍以匀速沿南偏东
海里的速度航行,当航行1小时后,甲在A处发现自己的渔具掉在乙船上,于是迅速改变航向和速度,仍以匀速沿南偏东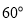 方向追赶乙船,正好在B处追上
方向追赶乙船,正好在B处追上 甲船追赶乙船的速度为多少海里
甲船追赶乙船的速度为多少海里 小时?
小时?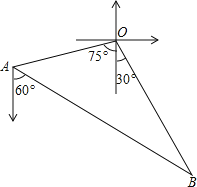
-
科目: 来源: 题型:
查看答案和解析>>【题目】“绿水青山,就是金山银山”.某旅游景区为了保护环境,需购买
 两种型号的垃圾处理设备共10台,已知每台
两种型号的垃圾处理设备共10台,已知每台 型设备日处理能力为12吨;每台
型设备日处理能力为12吨;每台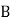 型设备日处理能力为15吨,购回的设备日处理能力不低于140吨.
型设备日处理能力为15吨,购回的设备日处理能力不低于140吨.(1)请你为该景区设计购买
 两种设备的方案;
两种设备的方案;(2)已知每台
 型设备价格为3万元,每台
型设备价格为3万元,每台 型设备价格为4.4万元.厂家为了促销产品,规定货款不低于40万元时,则按9折优惠;问:采用(1)设计的哪种方案,使购买费用最少,为什么?
型设备价格为4.4万元.厂家为了促销产品,规定货款不低于40万元时,则按9折优惠;问:采用(1)设计的哪种方案,使购买费用最少,为什么? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,点A、D是抛物线
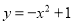 上两动点,点B、C在x轴上,且四边形ABCD是矩形,点E是抛物线与y轴的交点,连接BE交AD于点F,AD与y轴的交点为点G.设点A的横坐标为a(0<a<1).
上两动点,点B、C在x轴上,且四边形ABCD是矩形,点E是抛物线与y轴的交点,连接BE交AD于点F,AD与y轴的交点为点G.设点A的横坐标为a(0<a<1).(1) 若矩形ABCD的周长为3.5,求a的值;
(2) 求证:不论点A如何运动,∠EAD=∠ABE;
(3) 若△ABE是等腰三角形,
①求点A的坐标;
②如图2,若将直线BA绕点B按逆时针方向旋转至直线l,设点A、C到直线l的距离分别为
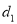 、
、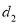 ,求
,求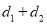 的最大值.
的最大值.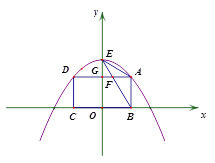
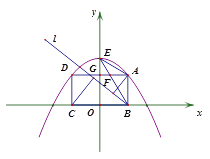
图1 图2
-
科目: 来源: 题型:
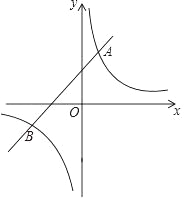
查看答案和解析>>【题目】如图,直线y1=x+2与双曲线y2=
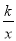 交于A(a,4),B(m,n).
交于A(a,4),B(m,n). (1)求k值和点B的坐标;
(2)求△AOB的面积;
(3)当y1>y2时请直接写出x的取值范围;
(4)P为x轴上任意一点,当△ABP为直角三角形时,直接写出P点坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】海水养殖是莱州经济产业的亮丽名片之一,某养殖场响应山东省加快新旧动能转换的号召,今年采用新技术投资养殖了200万笼扇贝,并且全部被订购,已知每笼扇贝的成本是40元,售价是100元,打捞出售过程中发现,一部分扇贝生长情况不合要求,最后只能按照25元一笼出售,如果纯收入为
 万元,不合要求的扇贝有
万元,不合要求的扇贝有 万笼.
万笼.(1)求纯收入
 关于
关于 的关系式.
的关系式.(2)当
 为何值时,养殖场不赔不嫌?
为何值时,养殖场不赔不嫌?
相关试题

