【题目】如图1,点A、D是抛物线![]() 上两动点,点B、C在x轴上,且四边形ABCD是矩形,点E是抛物线与y轴的交点,连接BE交AD于点F,AD与y轴的交点为点G.设点A的横坐标为a(0<a<1).
上两动点,点B、C在x轴上,且四边形ABCD是矩形,点E是抛物线与y轴的交点,连接BE交AD于点F,AD与y轴的交点为点G.设点A的横坐标为a(0<a<1).
(1) 若矩形ABCD的周长为3.5,求a的值;
(2) 求证:不论点A如何运动,∠EAD=∠ABE;
(3) 若△ABE是等腰三角形,
①求点A的坐标;
②如图2,若将直线BA绕点B按逆时针方向旋转至直线l,设点A、C到直线l的距离分别为![]() 、
、![]() ,求
,求![]() 的最大值.
的最大值.
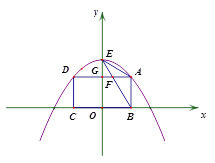
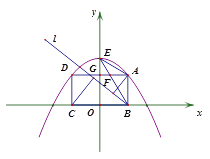
图1 图2
参考答案:
【答案】(1)a=0.5;(2) 见解析; (3)( ![]() ,
, ![]() )
) ![]()
【解析】试题分析:(1)由题意y轴是抛物线的对称轴,也是矩形ABCD的对称轴,根据矩形的周长列出方程即可解决问题;
(2)如图1中,首先构建二次函数证明![]() 再证明
再证明![]() 四点共圆,即可解决问题;
四点共圆,即可解决问题;
(3)①观察图形可知当![]() 是等腰三角形时,只有
是等腰三角形时,只有![]() 在
在![]() 中,根据
中,根据![]() 可得
可得![]() 求出
求出![]() 即可解决问题.
即可解决问题.
②如图3中,过点A作AM∥直线![]() ,
, ![]() 直线
直线![]() 于
于![]() ,
, ![]() 直线
直线![]() 于
于![]() ,延长
,延长![]() 交
交![]() 于
于![]() .则四边形
.则四边形![]() 是矩形,由
是矩形,由![]() 推出
推出![]() 欲求
欲求![]() 的最大值,只要求
的最大值,只要求![]() 的最大值即可,点
的最大值即可,点![]() 与点
与点![]() 重合时
重合时![]() 的值最大.
的值最大.
试题解析:(1)由题意![]() 轴是抛物线的对称轴,也是矩形ABCD的对称轴,
轴是抛物线的对称轴,也是矩形ABCD的对称轴,
∴![]() 关于
关于![]() 轴对称,
轴对称,![]()
![]()
由题意![]()
解得![]() 或
或![]() (舍去),
(舍去),![]()
(2)如图1中,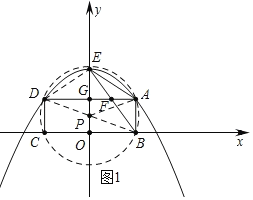
![]()
![]()
∴直线EB的解析式为![]()
直线DE的解析式为![]()
![]()
![]() 设BD交OE于P,
设BD交OE于P,
∵PG∥AB, ![]()
![]()
![]()
![]() 四点共圆,
四点共圆,
![]()
![]() =
= ![]() ,
,![]()
(3)观察图形可知当![]() 是等腰三角形时,只有
是等腰三角形时,只有![]()
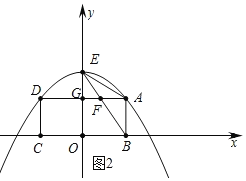
在![]() 中,
中, ![]()
![]()
解得![]() 或
或![]() (舍弃),
(舍弃),
∴点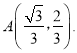
②如图3中,过点A作AM∥直线![]() ,
, ![]() 直线
直线![]() 于
于![]() ,
, ![]() 直线
直线![]() 于
于![]() ,延长
,延长![]() 交
交![]() 于
于![]() .则四边形
.则四边形![]() 是矩形,
是矩形,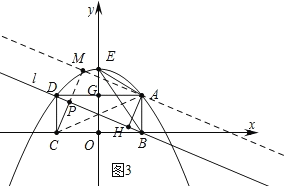
![]()
![]()
欲求![]()
![]() 的最大值即可,
的最大值即可,
在![]() 中,
中, ![]()
∴当点![]() 与点
与点![]() 重合时
重合时![]() 的值最大,此时
的值最大,此时![]()
![]() 的最大值
的最大值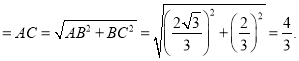
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,甲、乙两渔船同时从港口O出发外出捕鱼,乙沿南偏东
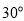 方向以每小时15海里的速度航行,甲沿南偏西
方向以每小时15海里的速度航行,甲沿南偏西 方向以每小时
方向以每小时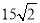 海里的速度航行,当航行1小时后,甲在A处发现自己的渔具掉在乙船上,于是迅速改变航向和速度,仍以匀速沿南偏东
海里的速度航行,当航行1小时后,甲在A处发现自己的渔具掉在乙船上,于是迅速改变航向和速度,仍以匀速沿南偏东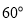 方向追赶乙船,正好在B处追上
方向追赶乙船,正好在B处追上 甲船追赶乙船的速度为多少海里
甲船追赶乙船的速度为多少海里 小时?
小时?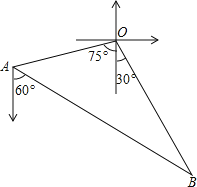
-
科目: 来源: 题型:
查看答案和解析>>【题目】“绿水青山,就是金山银山”.某旅游景区为了保护环境,需购买
 两种型号的垃圾处理设备共10台,已知每台
两种型号的垃圾处理设备共10台,已知每台 型设备日处理能力为12吨;每台
型设备日处理能力为12吨;每台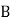 型设备日处理能力为15吨,购回的设备日处理能力不低于140吨.
型设备日处理能力为15吨,购回的设备日处理能力不低于140吨.(1)请你为该景区设计购买
 两种设备的方案;
两种设备的方案;(2)已知每台
 型设备价格为3万元,每台
型设备价格为3万元,每台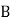 型设备价格为4.4万元.厂家为了促销产品,规定货款不低于40万元时,则按9折优惠;问:采用(1)设计的哪种方案,使购买费用最少,为什么?
型设备价格为4.4万元.厂家为了促销产品,规定货款不低于40万元时,则按9折优惠;问:采用(1)设计的哪种方案,使购买费用最少,为什么? -
科目: 来源: 题型:
查看答案和解析>>【题目】作图与计算:
在如图所示的正方形网格中,每个小正方形的边长为
 ,格点三角形(顶点是网格线的交点的三角形)
,格点三角形(顶点是网格线的交点的三角形) 的顶点
的顶点 ,
, 的坐标分别为
的坐标分别为 ,
, .
.
(1)请在如图所示的网格平面内作出平面直角坐标系;
(2)请作出
 关于
关于 轴对称的
轴对称的 ;
;(3)直接写出
 的面积及点
的面积及点 的坐标.
的坐标. -
科目: 来源: 题型:
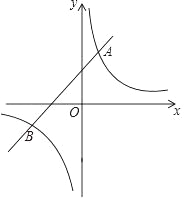
查看答案和解析>>【题目】如图,直线y1=x+2与双曲线y2=
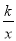 交于A(a,4),B(m,n).
交于A(a,4),B(m,n). (1)求k值和点B的坐标;
(2)求△AOB的面积;
(3)当y1>y2时请直接写出x的取值范围;
(4)P为x轴上任意一点,当△ABP为直角三角形时,直接写出P点坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】海水养殖是莱州经济产业的亮丽名片之一,某养殖场响应山东省加快新旧动能转换的号召,今年采用新技术投资养殖了200万笼扇贝,并且全部被订购,已知每笼扇贝的成本是40元,售价是100元,打捞出售过程中发现,一部分扇贝生长情况不合要求,最后只能按照25元一笼出售,如果纯收入为
 万元,不合要求的扇贝有
万元,不合要求的扇贝有 万笼.
万笼.(1)求纯收入
 关于
关于 的关系式.
的关系式.(2)当
 为何值时,养殖场不赔不嫌?
为何值时,养殖场不赔不嫌? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一楼房AB后有一假山,其坡度为i=1∶
 ,山坡坡面上E点处有一休息亭,测得假山坡脚C与楼房水平距离BC=25米,与亭子距离CE=20米,小丽从楼房顶测得E点的俯角为45°,求楼房AB的高度.(注:坡度i是指坡面的铅直高度与水平宽度的比)
,山坡坡面上E点处有一休息亭,测得假山坡脚C与楼房水平距离BC=25米,与亭子距离CE=20米,小丽从楼房顶测得E点的俯角为45°,求楼房AB的高度.(注:坡度i是指坡面的铅直高度与水平宽度的比)
相关试题

