【题目】已知△ABC中,∠ABC=45°,AB=7![]() ,BC=17,以AC为斜边在△ABC外作等腰Rt△ACD,连接BD,则BD的长为___.
,BC=17,以AC为斜边在△ABC外作等腰Rt△ACD,连接BD,则BD的长为___.
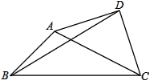
参考答案:
【答案】![]()
【解析】
显然直接求BD不好入手,那么就将问题进行转化.注意到△ACD为等腰Rt△,于是以AB为腰向左作等腰Rt△ABE,则易证△ABD与△AEC相似,相似比为![]() ,从而只需求出EC即可,此时∠EBC=135°,于是过E作EF⊥BC于F,则△EFB也为等腰Rt△,算出EF、BF,进而算出EC,问题迎刃而解.
,从而只需求出EC即可,此时∠EBC=135°,于是过E作EF⊥BC于F,则△EFB也为等腰Rt△,算出EF、BF,进而算出EC,问题迎刃而解.
以AB为腰作等腰Rt△ABE,连接EC,
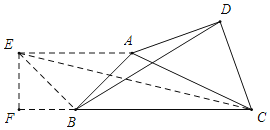
∵△ADC为等腰Rt△,
∴![]() ,∠EAB=∠DAC=45°,
,∠EAB=∠DAC=45°,
∴∠EAB+∠BAC=∠BAC+∠DAC,
∴∠EAC=∠DAB,
∴△EAC∽△BAD,
∴![]() ,
,
作EF⊥BC交BC延长线于F,
∵∠ABC=45°,∠EBA=90°,
∴∠EBF=45°,
∴△EFB为等腰Rt△,
∴EF=FB=![]() EB=
EB=![]() AB=7,
AB=7,
∴EC=![]() =25,
=25,
∴BD=![]() EC=
EC=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,△ABC内接于⊙O,AC是直径,点D是AC延长线上一点,且∠DBC=∠BAC,
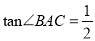 .
.(1) 求证:BD是⊙O的切线;
(2) 求
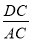 的值;
的值;(3) 如图2,过点B作BG⊥AC交AC于点F,交⊙O于点G,BC、AG的延长线交于点E,⊙O的半径为6,求BE的长.
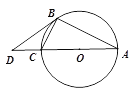
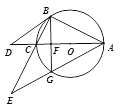
图1 图2
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是甲、乙两车在某时段速度随时间变化的图象,下列结论错误的是( )
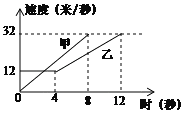
A. 乙前4秒行驶的路程为48米 B. 两车到第3秒时行驶的路程相等
C. 在0到8秒内甲的速度每秒增加4米/秒 D. 在4至8秒内甲的速度都大于乙的速度
-
科目: 来源: 题型:
查看答案和解析>>【题目】化简求值:
(1)当a=﹣1,b=2时,求代数式﹣2(ab﹣3b2)﹣[6b2﹣(ab﹣a2)]的值
(2)先化简,再求值:4xy﹣2(
 x2﹣3xy+2y2)+3(x2﹣2xy),当(x﹣3)2+|y+1|=0,求式子的值
x2﹣3xy+2y2)+3(x2﹣2xy),当(x﹣3)2+|y+1|=0,求式子的值(3)若(2mx2﹣x+3)﹣(3x2﹣x﹣4)的结果与x的取值无关,求m的值
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,甲、乙两渔船同时从港口O出发外出捕鱼,乙沿南偏东
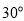 方向以每小时15海里的速度航行,甲沿南偏西
方向以每小时15海里的速度航行,甲沿南偏西 方向以每小时
方向以每小时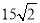 海里的速度航行,当航行1小时后,甲在A处发现自己的渔具掉在乙船上,于是迅速改变航向和速度,仍以匀速沿南偏东
海里的速度航行,当航行1小时后,甲在A处发现自己的渔具掉在乙船上,于是迅速改变航向和速度,仍以匀速沿南偏东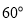 方向追赶乙船,正好在B处追上
方向追赶乙船,正好在B处追上 甲船追赶乙船的速度为多少海里
甲船追赶乙船的速度为多少海里 小时?
小时?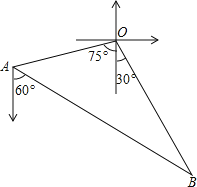
-
科目: 来源: 题型:
查看答案和解析>>【题目】“绿水青山,就是金山银山”.某旅游景区为了保护环境,需购买
 两种型号的垃圾处理设备共10台,已知每台
两种型号的垃圾处理设备共10台,已知每台 型设备日处理能力为12吨;每台
型设备日处理能力为12吨;每台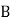 型设备日处理能力为15吨,购回的设备日处理能力不低于140吨.
型设备日处理能力为15吨,购回的设备日处理能力不低于140吨.(1)请你为该景区设计购买
 两种设备的方案;
两种设备的方案;(2)已知每台
 型设备价格为3万元,每台
型设备价格为3万元,每台 型设备价格为4.4万元.厂家为了促销产品,规定货款不低于40万元时,则按9折优惠;问:采用(1)设计的哪种方案,使购买费用最少,为什么?
型设备价格为4.4万元.厂家为了促销产品,规定货款不低于40万元时,则按9折优惠;问:采用(1)设计的哪种方案,使购买费用最少,为什么? -
科目: 来源: 题型:
查看答案和解析>>【题目】作图与计算:
在如图所示的正方形网格中,每个小正方形的边长为
 ,格点三角形(顶点是网格线的交点的三角形)
,格点三角形(顶点是网格线的交点的三角形) 的顶点
的顶点 ,
, 的坐标分别为
的坐标分别为 ,
, .
.
(1)请在如图所示的网格平面内作出平面直角坐标系;
(2)请作出
 关于
关于 轴对称的
轴对称的 ;
;(3)直接写出
 的面积及点
的面积及点 的坐标.
的坐标.
相关试题

