【题目】如图,将长方形ABCD沿直线BD折叠,使点C落在点C′处,BC′交AD于E,AD=8,AB=4.求△BED 的面积.

参考答案:
【答案】10.
【解析】试题分析:因为折叠前后∠DBC=∠DBC′,且因为平行,内错角相等,所以∠DCB=∠ADB,所以根据角之间的等量代换可知DE=BE,要想求出△BED的面积,只要求出DE即可,设DE=x,则AE=8-x,在Rt△ABE中由勾股定理可求得DE的长,进而求得△BED 的面积.
试题解析:∵△BDC′是由△BDC沿直线BD折叠得到的,∴∠C′BD=∠CBD,∵四边形ABCD是矩形,∴AD∥BC,∴∠CBD=∠EDB,∴∠C′BD=∠EDB,∴BE=DE,设DE=x,则AE=AD-DE=8-x,∵∠A=90°,BE=DE=x,∴![]() ,∴
,∴![]() ,∴x=5,∴△BED的面积=
,∴x=5,∴△BED的面积=![]() DE×AB=
DE×AB=![]() ×5×4=10.
×5×4=10.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校学生会准备调查七年级叙述参加“绘画类”、“书法类”、“乐器类”四类校本课程的人数,在全校进行随机抽样调查,并根据收集的数据绘制了如图两幅统计图(信息尚不完整),请根据图中提供的信息,解答下面的问题:
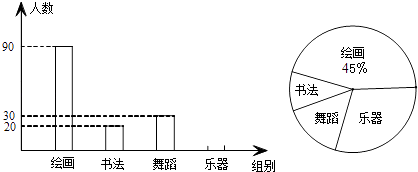
(1)此次共调查了多少名同学?
(2)将条形图补充完整,并计算扇形统计图中乐器部分的圆心角的度数;
(3)如果该校共有1000名学生参加这4个课外兴趣小组,而每个教师最多只能辅导本组的25名学生,估计书法兴趣小组至少需要准备多少名教师? -
科目: 来源: 题型:
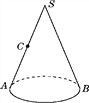
查看答案和解析>>【题目】已知:如图,观察图形回答下面的问题:
(1)此图形的名称为________.
(2)请你与同伴一起做一个这样的物体,并把它沿AS剪开,铺在桌面上,则它的侧面展开图是一个________.
(3)如果点C是SA的中点,在A处有一只蜗牛,在C处恰好有蜗牛想吃的食品,但它又不能直接沿AC爬到C处,只能沿此立体图形的表面爬行,你能在侧面展开图中画出蜗牛爬行的最短路线吗?
(4)SA的长为10,侧面展开图的圆心角为90°,请你求出蜗牛爬行的最短路程.
-
科目: 来源: 题型:
查看答案和解析>>【题目】高速公路的同一侧有A、B两城镇,如图,它们到高速公路所在直线MN的距离分别为AA′=2 km,BB′=4 km,A′B′=8 km.要在高速公路上A′、B′之间建一个出口P,使A、B两城镇到P的距离之和最小.求这个最短距离.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学七年一班、二班共有90名学生,如果从一班转出4名同学到二班,那么一班的学生人数是二班的80%,问两班原来各有多少名学生?
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算a2·a3的正确结果是( )
A.a5
B.a6
C.a8
D.a9 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠1+∠2=180°,∠3=∠B,试判断∠AED与∠C的大小关系,并证明你的结论.

解:∠C与∠AED相等,理由如下:
∵∠1+∠2=180°(已知),∠1+∠DFE=180°(邻补角定义)
∴∠2= . ( . ),
∴AB∥EF( . )
∴∠3= . ( . )
又∠B=∠3(已知)
∴∠B= . (等量代换)
∴DE∥BC( . )
∴∠C=∠AED( . ).
相关试题

