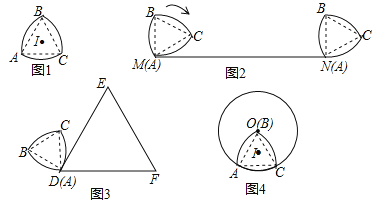
【题目】如图1,等边△ABC的边长为3,分别以顶点B、A、C为圆心,BA长为半径作![]() 、
、![]() 、
、![]() ,我们把这三条弧所组成的图形称作莱洛三角形,显然莱洛三角形仍然是轴对称图形,设点l为对称轴的交点.
,我们把这三条弧所组成的图形称作莱洛三角形,显然莱洛三角形仍然是轴对称图形,设点l为对称轴的交点.
(1)如图2,将这个图形的顶点A与线段MN作无滑动的滚动,当它滚动一周后点A与端点N重合,则线段MN的长为 ;
(2)如图3,将这个图形的顶点A与等边△DEF的顶点D重合,且AB⊥DE,DE=2π,将它沿等边△DEF的边作无滑动的滚动当它第一次回到起始位置时,求这个图形在运动过程中所扫过的区域的面积;
(3)如图4,将这个图形的顶点B与⊙O的圆心O重合,⊙O的半径为3,将它沿⊙O的圆周作无滑动的滚动,当它第n次回到起始位置时,点I所经过的路径长为 (请用含n的式子表示)
参考答案:
【答案】(1)3π;(2)27π;(3)2![]() nπ.
nπ.
【解析】试题分析:(1)先求出![]() 的弧长,继而得出莱洛三角形的周长为3π,即可得出结论;
的弧长,继而得出莱洛三角形的周长为3π,即可得出结论;
(2)先判断出莱洛三角形等边△DEF绕一周扫过的面积如图所示,利用矩形的面积和扇形的面积之和即可;
(3)先判断出莱洛三角形的一个顶点和O重合旋转一周点I的路径,再用圆的周长公式即可得出.
试题解析:解:(1)∵等边△ABC的边长为3,∴∠ABC=∠ACB=∠BAC=60°,![]() ,∴
,∴![]() =
=![]() =
=![]() =π,∴线段MN的长为
=π,∴线段MN的长为![]() =3π.故答案为:3π;
=3π.故答案为:3π;
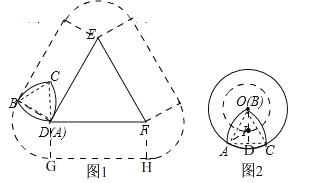
(2)如图1.∵等边△DEF的边长为2π,等边△ABC的边长为3,∴S矩形AGHF=2π×3=6π,由题意知,AB⊥DE,AG⊥AF,∴∠BAG=120°,∴S扇形BAG=![]() =3π,∴图形在运动过程中所扫过的区域的面积为3(S矩形AGHF+S扇形BAG)=3(6π+3π)=27π;
=3π,∴图形在运动过程中所扫过的区域的面积为3(S矩形AGHF+S扇形BAG)=3(6π+3π)=27π;
(3)如图2,连接BI并延长交AC于D.∵I是△ABC的重心也是内心,∴∠DAI=30°,AD=![]() AC=
AC=![]() ,∴OI=AI=
,∴OI=AI=![]() =
=![]() ,∴当它第1次回到起始位置时,点I所经过的路径是以O为圆心,OI为半径的圆周,∴当它第n次回到起始位置时,点I所经过的路径长为n2π
,∴当它第1次回到起始位置时,点I所经过的路径是以O为圆心,OI为半径的圆周,∴当它第n次回到起始位置时,点I所经过的路径长为n2π![]() =2
=2![]() nπ.故答案为:2
nπ.故答案为:2![]() nπ.
nπ.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,抛物线y=mx2﹣2mx+n(m<0)的顶点为A,与x轴交于B,C两点(点B在点C左侧),与y轴正半轴交于点D,连接AD并延长交x轴于E,连AC、DC.S△DEC:S△AEC=3:4.
(1)求点E的坐标;
(2)△AEC能否为直角三角形?若能,求出此时抛物线的函数表达式;若不能,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图:图形都是由面积为1的正方形按一定的规律组成,其中第(1)个图形中面积为1的正方形有9个,第(2)个图形中面积为1的正方形有14个,…,按此规律.则第(9)个图形中面积为1的正方形的个数为( )
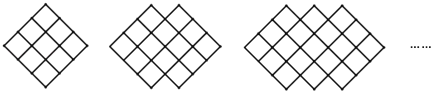
A.49B.45C.54D.50
-
科目: 来源: 题型:
查看答案和解析>>【题目】某厂接到遵义市一所中学的冬季校服订做任务,计划用A、B两台大型设备进行加工.如果单独用A型设备需要90天做完,如果单独用B型设备需要60天做完,为了同学们能及时领到冬季校服,工厂决定由两台设备同时赶制.
(1)两台设备同时加工,共需多少天才能完成?
(2)若两台设备同时加工30天后,B型设备出了故障,暂时不能工作,此时离发冬季校服时间还有13天.如果由A型设备单独完成剩下的任务,会不会影响学校发校服的时间?请通过计算说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平行四边形ABCD中,∠B=60°,AB=8cm,AD=10cm,点P在边BC上从B向C运动,点Q在边DA上从D向A运动,如果P,Q运动的速度都为每秒1cm,那么当运动时间t=_____秒时,四边形ABPQ是直角梯形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点
 、
、 、
、 是数轴上三点,点
是数轴上三点,点 表示的数为
表示的数为 ,
,  ,
,  .
.(
 )写出数轴上点
)写出数轴上点 、
、 表示的数:__________,__________.
表示的数:__________,__________.(
 )动点
)动点 ,
,  同时从
同时从 ,
,  出发,点
出发,点 以每秒
以每秒 个单位长度的速度沿数轴向右匀速运动,点
个单位长度的速度沿数轴向右匀速运动,点 以
以 个单位长度的速度沿数向左匀速运动,设运动时间为
个单位长度的速度沿数向左匀速运动,设运动时间为 秒.
秒.①求数轴上点
 ,
,  表示的数(用含
表示的数(用含 的式子表示);
的式子表示);②
 为何值时,点
为何值时,点 ,
,  相距
相距 个单位长度.
个单位长度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图.在△ABC中,∠C=90°,AC=BC,AB=30cm,点P在AB上,AP=10cm,点E从点P出发沿线段PA以2cm/s的速度向点A运动,同时点F从点P出发沿线段PB以1cm/s的速度向点B运动,点E到达点A后立刻以原速度沿线段AB向点B运动,在点E、F运动过程中,以EF为边作正方形EFGH,使它与△ABC在线段AB的同侧,设点E、F运动的时间为t(s)(0<t<20).
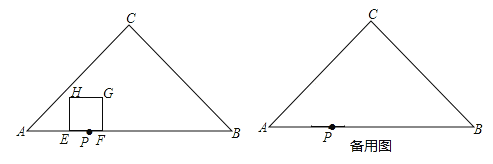
(1)当点H落在AC边上时,求t的值;
(2)设正方形EFGH与△ABC重叠部分的面积为S.①试求S关于t的函数表达式;②以点C为圆心,
 t为半径作⊙C,当⊙C与GH所在的直线相切时,求此时S的值.
t为半径作⊙C,当⊙C与GH所在的直线相切时,求此时S的值.
相关试题

