【题目】如图,在直角坐标系中,点A,B分别在x轴,y轴上,点A的坐标为(﹣1,0),∠ABO=30°,线段PQ的端点P从点O出发,沿△OBA的边按O→B→A→O运动一周,同时另一端点Q随之在x轴的非负半轴上运动,如果PQ= ![]() ,那么当点P运动一周时,点Q运动的总路程为 .
,那么当点P运动一周时,点Q运动的总路程为 . 
参考答案:
【答案】4
【解析】解:在Rt△AOB中,∵∠ABO=30°,AO=1, ∴AB=2,BO= ![]() =
= ![]() ,
,
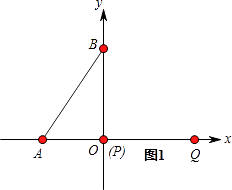
①当点P从O→B时,如图1、图2所示,点Q运动的路程为 ![]() ,
,
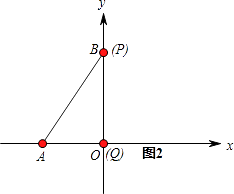
②如图3所示,QC⊥AB,则∠ACQ=90°,即PQ运动到与AB垂直时,垂足为P,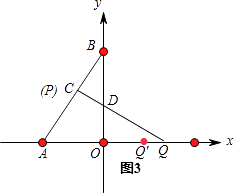
当点P从B→C时,
∵∠ABO=30°
∴∠BAO=60°
∴∠OQD=90°﹣60°=30°
∴cos30°= ![]()
∴AQ= ![]() =2
=2
∴OQ=2﹣1=1
则点Q运动的路程为QO=1,
③当点P从C→A时,如图3所示,点Q运动的路程为QQ′=2﹣ ![]() ,
,
④当点P从A→O时,点Q运动的路程为AO=1,
∴点Q运动的总路程为: ![]() +1+2﹣
+1+2﹣ ![]() +1=4
+1=4
故答案为:4
首先根据题意正确画出从O→B→A运动一周的图形,分四种情况进行计算:①点P从O→B时,路程是线段PQ的长;②当点P从B→C时(QC⊥AB,C为垂足),点Q从O运动到Q,计算OQ的长就是运动的路程;③点P从C→A时,点Q由Q向左运动,路程为QQ′;④点P从A→O时,点Q运动的路程就是点P运动的路程;最后相加即可.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A和点B都在反比例函数y=
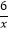 的图象上,且线段AB过原点,过点A作x轴的垂线段,垂足为C,P是线段OB上的动点,连接CP.设△ACP的面积为S,则下列说法正确的是( )
的图象上,且线段AB过原点,过点A作x轴的垂线段,垂足为C,P是线段OB上的动点,连接CP.设△ACP的面积为S,则下列说法正确的是( ) 
A.S>3
B.S>6
C.3≤S≤6
D.3<S≤6 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在一次数学课外实践活动中,小聪在距离旗杆10m的A处测得旗杆顶端B的仰角为60°,测角仪高AD为1m,则旗杆高BC为 m(结果保留根号).

-
科目: 来源: 题型:
查看答案和解析>>【题目】现有三张分别标有数字1、2、6的卡片,它们除了数字外完全相同,把卡片背面朝上洗匀,从中任意抽取一张,将上面的数字记为a(不放回),再从中任意抽取一张,将上面的数字记为b,这样的数字a,b能使关于x的一元二次方程x2﹣2(a﹣3)x﹣b2+9=0有两个正根的概率为
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们知道,图形是一种重要的数学语言,它直观形象,能有效地表现一些代数中的数量关系,对几何图形做出代数解释和用几何图形的面积表示代数恒等式是互逆的.课本上由拼图用几何图形的面积来验证了乘法公式,一些代数恒等式也能用这种形式表示,例如(2a+b)(a+b)=2a2+3ab+b2就可以用图①或图②等图形的面积表示.
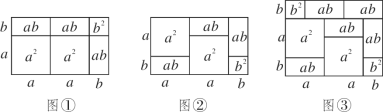
(1)填一填:请写出图③所表示的代数恒等式:______________________________;
(2)画一画:试画出一个几何图形,使它的面积能表示:(a+b)(a+3b)=a2+4ab+3b2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,边长为4的正方形ABCD内接于点O,点E是
 上的一动点(不与A、B重合),点F是
上的一动点(不与A、B重合),点F是  上的一点,连接OE、OF,分别与AB、BC交于点G,H,且∠EOF=90°,有以下结论: ①
上的一点,连接OE、OF,分别与AB、BC交于点G,H,且∠EOF=90°,有以下结论: ①  =
=  ;
;
②△OGH是等腰三角形;
③四边形OGBH的面积随着点E位置的变化而变化;
④△GBH周长的最小值为4+ .
.
其中正确的是(把你认为正确结论的序号都填上).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,港口B位于港口O正西方向120km处,小岛C位于港口O北偏西60°的方向.一艘游船从港口O出发,沿OA方向(北偏西30°)以vkm/h的速度驶离港口O,同时一艘快艇从港口B出发,沿北偏东30°的方向以60km/h的速度驶向小岛C,在小岛C用1h加装补给物资后,立即按原来的速度给游船送去.
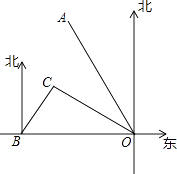
(1)快艇从港口B到小岛C需要多长时间?
(2)若快艇从小岛C到与游船相遇恰好用时1h,求v的值及相遇处与港口O的距离.
相关试题

