【题目】如图,C为线段AE上一动点(不与A、E重合),在AE同侧分别作等边△ABC和等边△CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ,以下五个结论:①AD=BE;②PQ∥AE;③CP=CQ;④BO=OE;⑤∠AOB=60°,恒成立的结论有

A. ①③⑤ B. ①③④⑤ C. ①②③⑤ D. ①②③④⑤
参考答案:
【答案】C
【解析】
①根据全等三角形的判定方法,证出△ACD≌△BCE,即可得出AD=BE.
③先证明△ACP≌△BCQ,即可判断出CP=CQ,③正确;
②根据∠PCQ=60°,可得△PCQ为等边三角形,证出∠PQC=∠DCE=60°,得出PQ∥AE,②正确.
④没有条件证出BO=OE,得出④错误;
⑤∠AOB=∠DAE+∠AEO=∠DAE+∠ADC=∠DCE=60°,⑤正确;即可得出结论.
∵△ABC和△CDE都是等边三角形,
∴AC=BC,CD=CE,∠ACB=∠DCE=60,
∴∠ACB+∠BCD=∠DCE+∠BCD,
∴∠ACD=∠BCE,
在△ACD和△BCE中,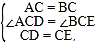
∴△ACD≌△BCE(SAS),
∴AD=BE,结论①正确,
∵△ACD≌△BCE,
∴∠CAD=∠CBE,
又∵![]()
∴![]()
∴![]()
在△ACP和△BCQ中,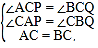
∴△ACP≌△BCQ(AAS),
∴CP=CQ,结论③正确;
又∵![]()
∴△PCQ为等边三角形,
∴![]()
∴PQ∥AE,结论②正确,
∵△ACD≌△BCE,
∴∠ADC=∠AEO,
∴![]()
∴结论⑤正确.没有条件证出BO=OE,④错误;
综上,可得正确的结论有4个:①②③⑤.
故选:C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,在平面直角坐标系中,二次函数y=﹣
 x2+bx+c的图象与坐标轴交于A,B,C三点,其中点A的坐标为(﹣3,0),点B的坐标为(4,0),连接AC,BC.动点P从点A出发,在线段AC上以每秒1个单位长度的速度向点C作匀速运动;同时,动点Q从点O出发,在线段OB上以每秒1个单位长度的速度向点B作匀速运动,当其中一点到达终点时,另一点随之停止运动,设运动时间为t秒.连接PQ.
x2+bx+c的图象与坐标轴交于A,B,C三点,其中点A的坐标为(﹣3,0),点B的坐标为(4,0),连接AC,BC.动点P从点A出发,在线段AC上以每秒1个单位长度的速度向点C作匀速运动;同时,动点Q从点O出发,在线段OB上以每秒1个单位长度的速度向点B作匀速运动,当其中一点到达终点时,另一点随之停止运动,设运动时间为t秒.连接PQ.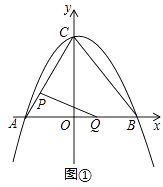
(1)填空:b= , c=;
(2)在点P,Q运动过程中,△APQ可能是直角三角形吗?请说明理由;
(3)在x轴下方,该二次函数的图象上是否存在点M,使△PQM是以点P为直角顶点的等腰直角三角形?若存在,请求出运动时间t;若不存在,请说明理由;
(4)如图②,点N的坐标为(﹣ ,0),线段PQ的中点为H,连接NH,当点Q关于直线NH的对称点Q′恰好落在线段BC上时,请直接写出点Q′的坐标.
,0),线段PQ的中点为H,连接NH,当点Q关于直线NH的对称点Q′恰好落在线段BC上时,请直接写出点Q′的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,将两个完全相同的三角形纸片ABC和DEC重合放置,其中∠C=900,∠B=∠E=300.



(1)操作发现如图2,固定△ABC,使△DEC绕点C旋转。当点D恰好落在BC边上时,填空:线段DE与AC的位置关系是 ;
② 设△BDC的面积为S1,△AEC的面积为S2。则S1与S2的数量关系是 。
(2)猜想论证
当△DEC绕点C旋转到图3所示的位置时,小明猜想(1)中S1与S2的数量关系仍然成立,并尝试分别作出了△BDC和△AEC中BC,CE边上的高,请你证明小明的猜想。
(3)拓展探究
已知∠ABC=600,点D是其角平分线上一点,BD=CD=4,OE∥AB交BC于点E(如图4),若在射线BA上存在点F,使S△DCF =S△BDC,请直接写出相应的BF的长
-
科目: 来源: 题型:
查看答案和解析>>【题目】【问题提出】如图①,已知海岛A到海岸公路BD的距离为AB,C为公路BD上的酒店,从海岛A到酒店C,先乘船到登陆点D,船速为a,再乘汽车,车速为船速的n倍,点D选在何处时,所用时间最短?
【特例分析】若n=2,则时间t=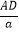 +
+ 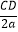 ,当a为定值时,问题转化为:在BC上确定一点D,使得AD+
,当a为定值时,问题转化为:在BC上确定一点D,使得AD+ 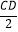 的值最小.如图②,过点C做射线CM,使得∠BCM=30°.
的值最小.如图②,过点C做射线CM,使得∠BCM=30°.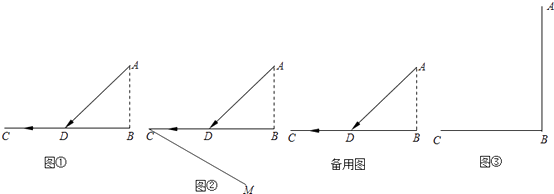
(1)过点D作DE⊥CM,垂足为E,试说明:DE=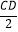 ;
;
(2)【问题解决】请在图②中画出所用时间最短的登陆点D′,并说明理由.
(3)【模型运用】请你仿照“特例分析”中的相关步骤,解决图①中的问题(写出具体方案,如相关图形呈现、图形中角所满足的条件、作图的方法等).
(4)如图③,海面上一标志A到海岸BC的距离AB=300m,BC=300m.救生员在C点处发现标志A处有人求救,
立刻前去营救,若救生员在岸上跑的速度都是6m/s,在海中游泳的速度都是2m/s,求救生员从C点出发到
达A处的最短时间. -
科目: 来源: 题型:
查看答案和解析>>【题目】完成下面推理过程:

如图,已知∠1 =∠2,∠B =∠C,可推得AB∥CD.理由如下:
∵∠1 =∠2(已知),
且∠1 =∠CGD(______________ _________),
∴∠2 =∠CGD(等量代换).
∴CE∥BF(___________________ ________).
∴∠ =∠C(__________________________).
又∵∠B =∠C(已知),
∴∠ =∠B(等量代换).
∴AB∥CD(________________________________).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC周长为1,连接△ABC三边中点构成第二个三角形,再连接第二个三角形三边中点构成第三个三角形,以此类推,第2 016个三角形的周长为( )
A. 22 016 B. 22 017 C. (
 )2 016 D. (
)2 016 D. ( )2 015
)2 015 -
科目: 来源: 题型:
查看答案和解析>>【题目】点C在直线AB上,AC=10cm,CB=8cm,点M、N分别是AC、BC的中点,则线段MN的长为______.
相关试题

