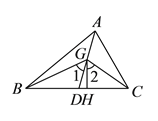
【题目】如图,在![]() 中,
中, ![]() 是它的角平分线,
是它的角平分线, ![]() 是
是![]() 上的一点,
上的一点, ![]() ,
, ![]() 分别平分
分别平分![]() ,
, ![]() ,
, ![]() ,垂足为点
,垂足为点![]() .
.
求证:( ![]() )
)![]() .(
.(![]() )
)![]() .
.
参考答案:
【答案】见解析.
【解析】试题分析:(1)由三角形内角和定理可知∠ABC+∠ACB=180°﹣∠BAC,然后利用角平分线的性质即可求出∠BGC=90°+![]() ∠BAC.
∠BAC.
(2)由AD是角平分线,得到∠BAD=∠CAD,然后根据图形可知:∠1=∠BAD+∠ABG,∠2=90°﹣∠GCH,最后根据三角形的内角和定理以及外角的性质即可求出答案.
试题解析:解:(1)由三角形内角和定理可知:∠ABC+∠ACB=180°﹣∠BAC.∵BG,CG分别平分∠ABC,∠ACB,∠GBC=![]() ∠ABC,∠GCB=
∠ABC,∠GCB=![]() ∠ACB,∴∠GBC+∠GCB=
∠ACB,∴∠GBC+∠GCB=![]() (∠ABC+∠ACB)=
(∠ABC+∠ACB)=![]() (180°﹣∠BAC)=90°﹣
(180°﹣∠BAC)=90°﹣![]() ∠BAC,∴∠BGC=180°﹣(∠GBC+∠GCB)=180°﹣
∠BAC,∴∠BGC=180°﹣(∠GBC+∠GCB)=180°﹣![]() (∠ABC+∠ACB)=90°+
(∠ABC+∠ACB)=90°+![]() ∠BAC;
∠BAC;
(2)∵AD是它的角平分线,∴∠BAD=∠CAD,∴∠1=∠BAD+∠ABG.∵GH⊥BC,∴∠GHC=90°,∴∠2=90°﹣∠GCH=90°﹣![]() ∠ACB=90°﹣
∠ACB=90°﹣![]() (180°﹣∠DAC﹣∠ADC)
(180°﹣∠DAC﹣∠ADC)
=![]() ∠DAC+
∠DAC+![]() ∠ADC.
∠ADC.
∵∠ADC=∠ABC+∠BAD,∴ ![]() ∠ADC=
∠ADC=![]() ∠ABC+∠
∠ABC+∠![]() ∠BAD=∠ABG+
∠BAD=∠ABG+![]() ∠BAD,∴∠2=
∠BAD,∴∠2=![]() ∠DAC+
∠DAC+![]() ∠ADC=
∠ADC=![]() ∠BAD+
∠BAD+![]() ∠BAD+∠ABG=∠BAD+∠ABG,∴∠1=∠2.
∠BAD+∠ABG=∠BAD+∠ABG,∴∠1=∠2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若将点A(1,3)向左平移2个单位长度,再向下平移4个单位长度得到点B,则点B的坐标为( )
A.(-2,-1)B.(-1,0)C.(-1,-1)D.(-2,0)
-
科目: 来源: 题型:
查看答案和解析>>【题目】完成证明并写出推理根据:
已知,如图,∠1=132°,∠ACB=48°,∠2=∠3.
求证:∠CDB=∠FHB.
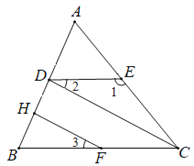
证明:
∵∠1=132°,∠ACB=48° (已知)
∴∠1+∠ACB=180°
∴DE∥BC ( )
∴∠2=∠ ( )
又∵∠2=∠3 (已知)
∴∠3=∠ (等量代换)
∴HF∥DC ( )
∴∠CDB=∠FHB ( )
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了了解某校学生进行课外阅读的情况,从全校2200名学生中随机抽取了100名学生,对他们平均每天进行课外阅读的时长进行统计,样本容量是_______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,AD是角平分线,BE平分∠ABC交AD于点E,点O在AB上,以OB为半径的⊙O经过点E,交AB于点F

(1)求证:AD是⊙O的切线;
(2)若AC=4,∠C=30°,求 的长.
的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】某市2009年元旦的最高气温为12℃,最低气温为-2℃,那么这天的最高气温比最低气温高 ( )
A.-14℃B.-10℃C.14℃D.10℃
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在平面直径坐标系中,抛物线y=ax2+bx﹣2与x轴交于点A(﹣3,0).B(1,0),与y轴交于点C
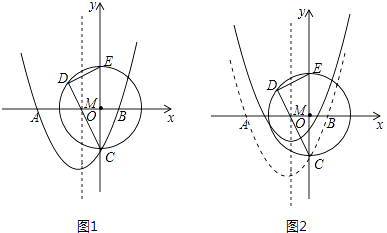
(1)直接写出抛物线的函数解析式;
(2)以OC为半径的⊙O与y轴的正半轴交于点E,若弦CD过AB的中点M,试求出DC的长;
(3)将抛物线向上平移 个单位长度(如图2)若动点P(x,y)在平移后的抛物线上,且点P在第三象限,请求出△PDE的面积关于x的函数关系式,并写出△PDE面积的最大值.
个单位长度(如图2)若动点P(x,y)在平移后的抛物线上,且点P在第三象限,请求出△PDE的面积关于x的函数关系式,并写出△PDE面积的最大值.
相关试题

